大家都这么说，那反过来可以吗？🤔

有时，反过来看问题，别有洞天。

人生反过来看看

人生只有两种悲剧，一是没有得到想要的东西，另一是得到了想要的东西。

——王尔德

人生有两种快乐，一是没有得到想要的东西，另一是得到了想要的东西。

——周国平

周国平反过来看王尔德的话，引申另一番思考。王尔德的立足点是占有，周国平的立足点是创造。当心态是占有时，未占有则心生痛苦，占有则心生空虚，横竖都是难受。当心态是创造时，未得到可以继续创造，得到可以品味和体验，横竖都是新奇。更重要的是，换成创造的心态之后，得失心没有那么重了，不再因为未得到而郁郁寡欢，一旦失去就一蹶不振，反而是更勇敢了，心胸更宽广了，接受没有得到的，感恩已经得到的。人生，需要反过来看看，你可以更释然，众人期许你，要成功，要出众，要…..，做到还好，做不到便深度怀疑自己，那不很亏。

经验反过来看看

杨振宁和李政道的灵光一闪，诺奖论文《弱相互作用中的宇称守恒质疑》，只花了两个月左右，1956年6月底论文写完，10月初论文发表。

杨振宁反过来看宇称守恒，发表诺奖论文。

宇称守恒是一条在“当时被广泛认可的物理定律”里，可以理解为“物理过程遵守镜像对称”，一个物理系统跟它的镜像，应该能遵守同样的物理定律，形成左右对称的过程。镜像对称，天经地义。在此前的无数物理实验里，“宇称守恒”也从未让物理学家们失望。这就是为什么许多物理学家不愿质疑这条规则。拿了1945年诺奖的著名毒舌物理学家泡利就说，“我不相信上帝是个左撇子。”著名的费曼也劝过想做实验检验此规则的拉姆齐说，“那是个疯狂的实验，不要在那上面浪费时间。”费曼还建议以10000 : 1来赌这个实验绝不会成功。

与大多数物理学家背道而驰，提出“宇称可能不守恒”就需要足够的勇气了。有了想法之后，至于怎么证明“宇称发生了不守恒”，他们只花了三星期，做了大量的计算，再做一些针对性的新实验，就能知道，弱相互作用不遵从“宇称守恒”。做科研，需要反过来看看，试一试嘛，如周国平先生所说，没得到期许的结果又不掉一块肉，万一是对的呢。

定理反过来看看

《欧式几何》中的五大公设：

1. 过相异两点，能作且只能作一直线。
2. 线段(有限直线)可以任意地延长。
3. 以任一点为圆心、任意长为半径，可作一圆。
4. 凡是直角都相等。
5. 过直线之外一点有唯一的一条直线和已知直线平行。

人人都想通过前四条定理证明第五条不像定理的定理，罗巴切夫斯基反过来看，它只是公设无需证明，如果你遵守这个游戏规则那就一块玩，当然你也可以改变规则，于是他将第五条公设改为过直线之外的一点至少有两条直线和已知直线平行，创立“非欧式几何”。

欧式几何是在平坦的空间结构背景下，而非欧几何关注弯曲空间下的几何结构。非欧式几何的创立为爱因斯坦发展广义相对论提供了思想基础和有力工具，而相对论给物理学带来了一场深刻的革命，动摇了牛顿力学在物理学中的统治地位，使人们对客观世界的认识产生了质的飞跃。

举一个简单的例子，三角形的内角和一定是180度吗？这在欧式几何是成立的，即在平坦空间里是成立的，但是在弯曲空间里就不成立。

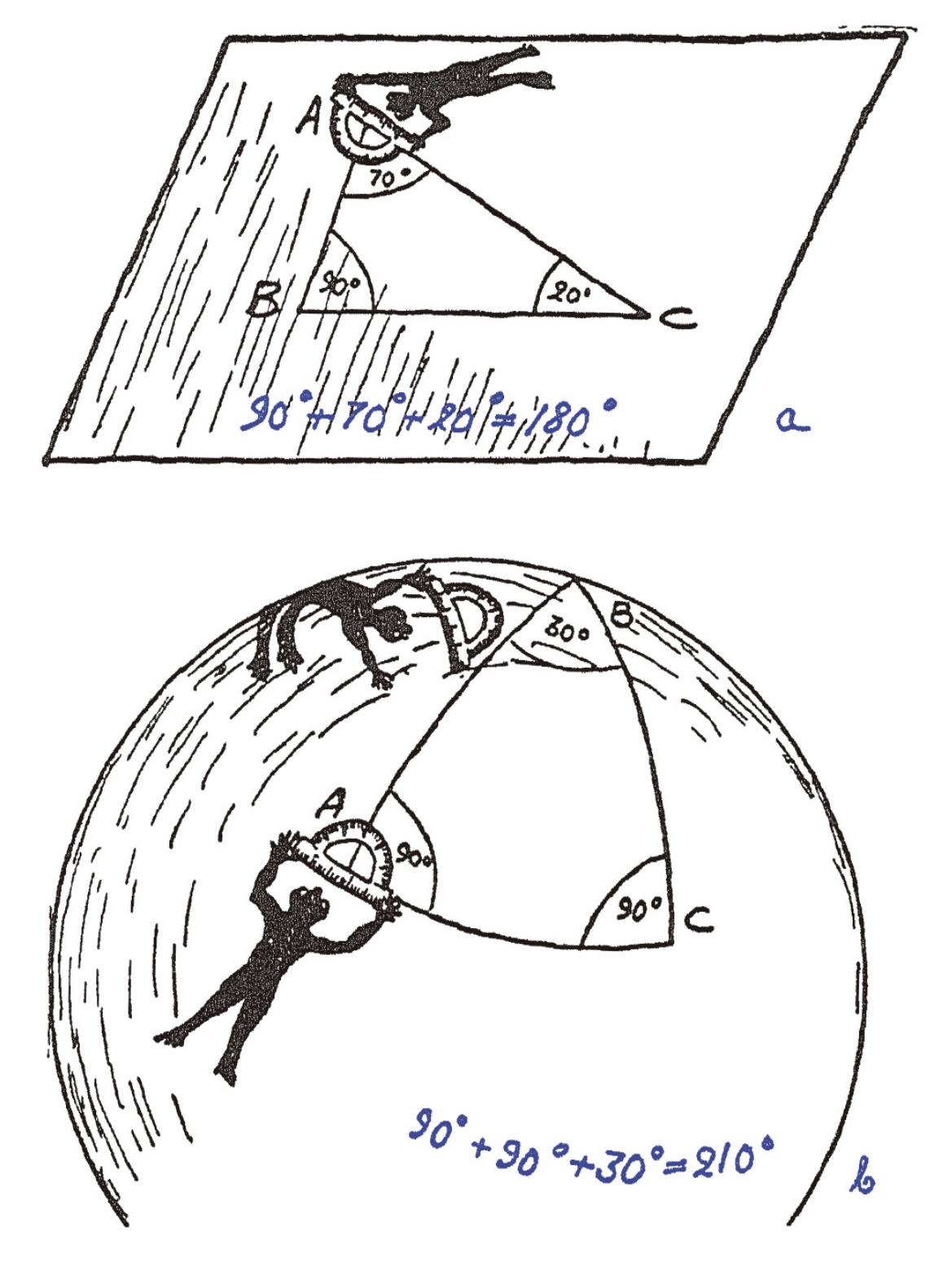
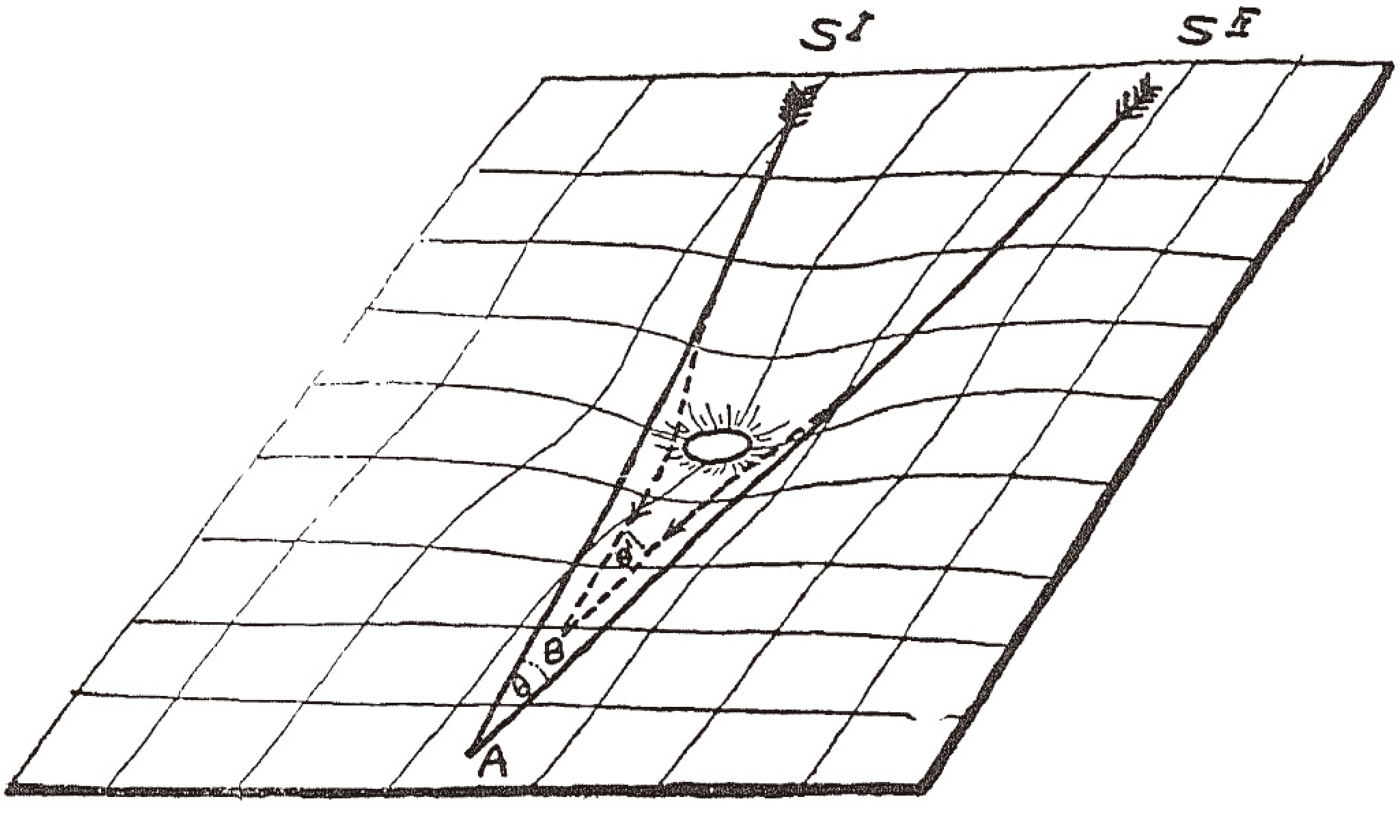
那我们生活的三维空间是平坦的还是弯曲的？验证想法很简单，在空间中的三点之间拉几条绳子，由此得到一个三角形，然后看看它的内角和是否等于180度不就好了。爱因斯坦提出一个假设：大质量物体附近的物理空间会变得弯曲，也就是说，我们在地球和另外两颗恒星之间拉三条绳子，把太阳围起来，那么你会发现，这个三角形的内角和明显不等于180度。为了验证这个猜想，找到合适的可观测的行星，我们需要挑选一个好日子，哪怕是白天，空中的恒星也清晰可见，不被太阳光遮挡，那就是日全食当天。1919年英国一支天文学小队长来到了西非的普林西比岛，这个地方是那一年观测日全食的最佳地点，测量结果验证了爱因斯坦的猜想。非欧几何更贴近真相，我们生活在弯曲的三维空间，那到底是局部弯曲还是全局弯曲？可以看看这里。

做理论，反过来看看，举手创造新的理论大厦，比之前那座更辉煌。

寻常观点反过来看看

寻常观点很多很多，比如，你不要拿自己长处跟别人短处比，比赢了也没什么，你要拿自己短板跟别人长处比，这样都比赢了，你就是真的厉害。

反过来看的话呢，就是，你大可以拿自己长处跟别人的短处比，这样你才知道自己是谁，天赋在哪里，而不陷入循环的自卑（此处应该也可以抬杠，就是说，自己的长处也比不过别人的短处，这真的是有的，那就换个参照物吧，哈哈）。刚看过《地球动脉》第一季，里面有三处激烈的场景，狼捕羊，鲨鱼捕海狗，鬣狗捕鹿。狼爆发力强，但是羊的奔跑速度很快，只要一门心思往前跑，一定可以逃脱狼口；鲨鱼有力量，但是海狗灵活呀，鲨鱼游的快但是转弯不行呀，只要海狗不放弃跟鲨鱼转圈子，鲨鱼也耐他不合；鬣狗是有耐力，但鹿有捕捉微弱声音的耳朵，不放松警惕，关键时候也可以救自己一命呀。

当我试着反过来看问题的时候，我发现很多专家说的东西就是跟大众唱反调的，比如

• 《黑客与画家》里说的“在现代社会中，收入差距拉大实际上是一种健康的信号？”
• 著名心理学家武志红说：“亲如母女，不是最好的婆媳关系。”
• 心理咨询师徐慢慢说：“如何拥有一段好关系？学会按时生气。”
• 我的老师说：“做菜的油烟比抽烟的烟吸入肺里更多。”

$\vdots$

总结

我们生在这片泥泞里，有时要跳脱出来是有点难，跳出世俗的观点，有些还真的是很优秀的人才能做得到（为什么不是跳脱了之后优秀呢🤔，哈哈，随时反过来想想），但是呢，作为普通的大众，我觉得自己起码可以意识到，我可以这么去想，可以这么去思考问题，错了就错了，又不打紧。