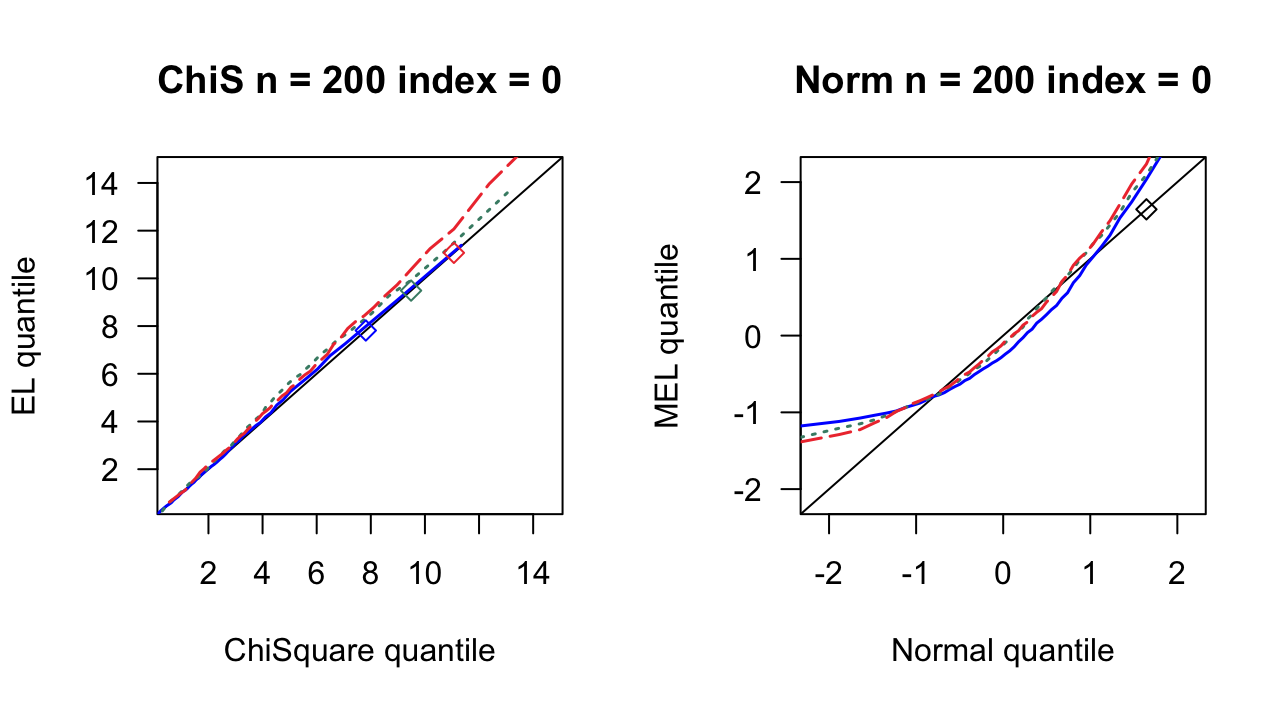
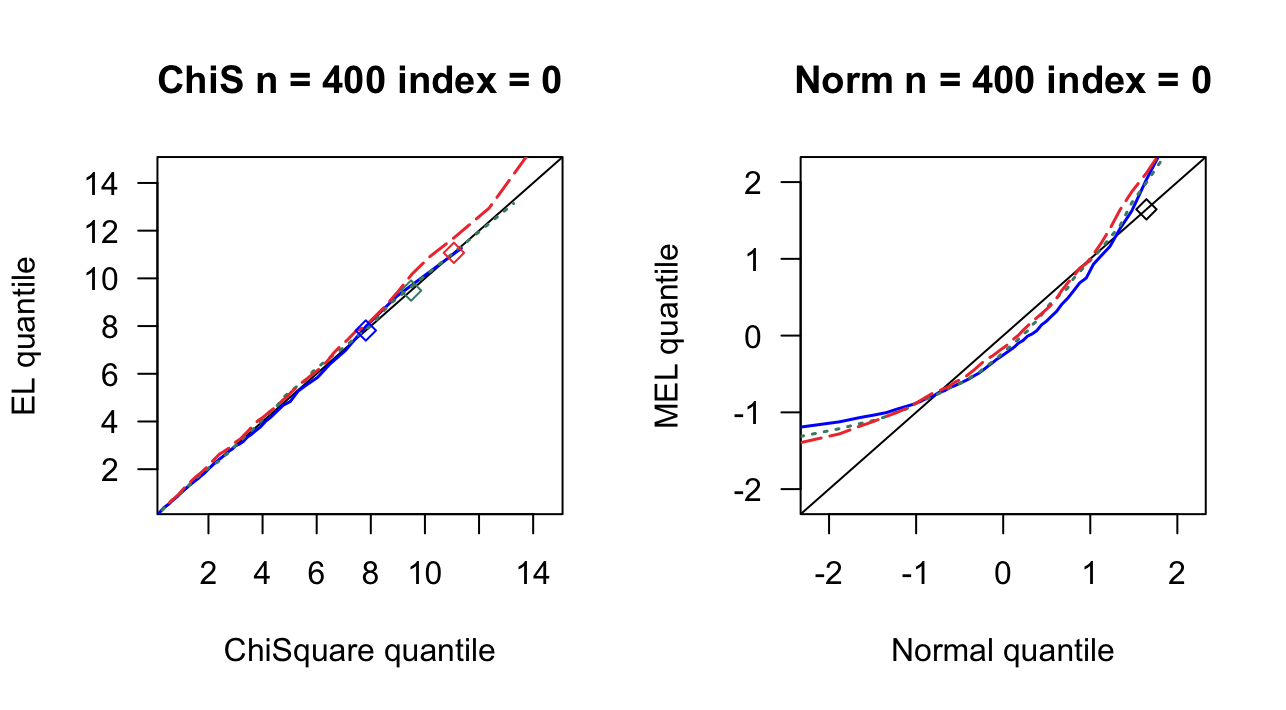
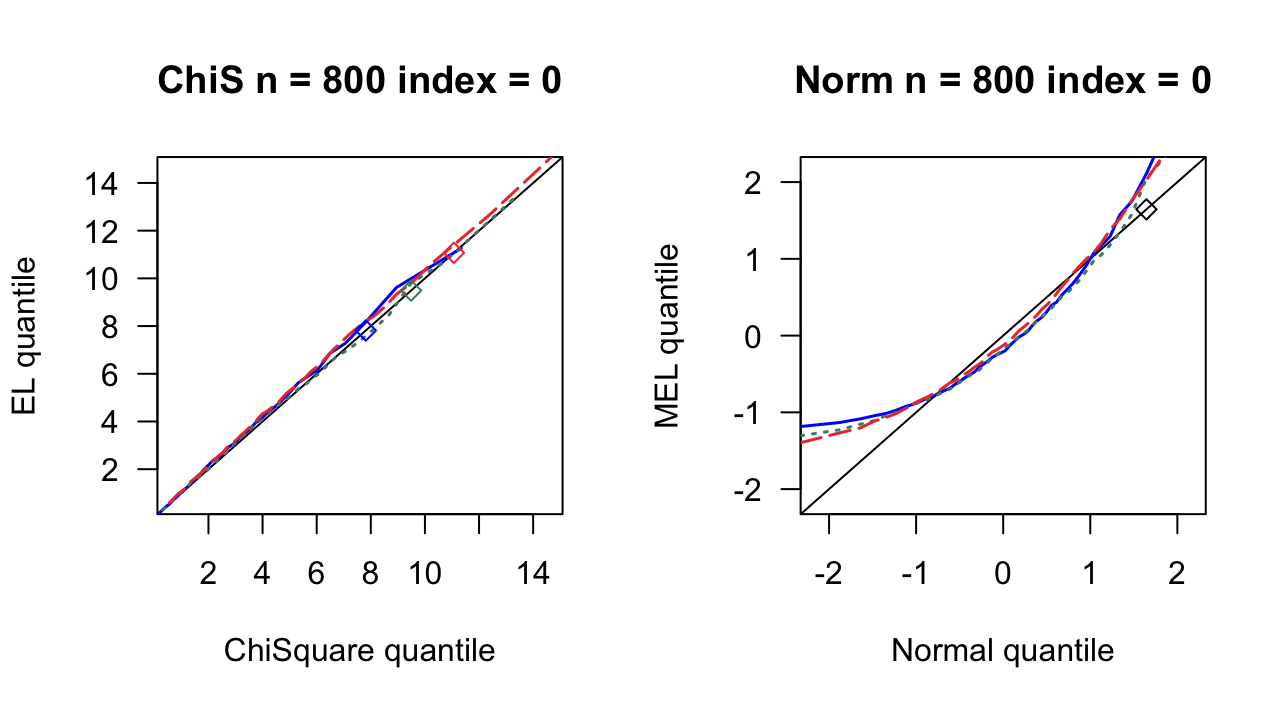
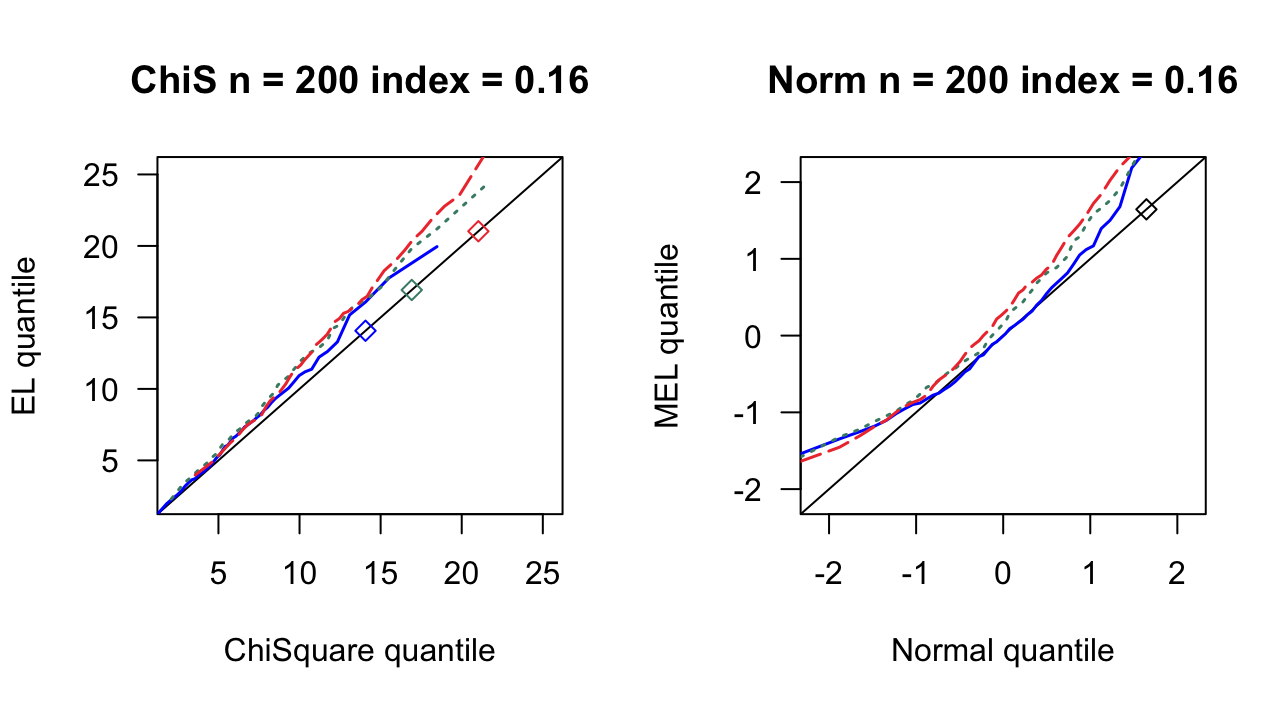
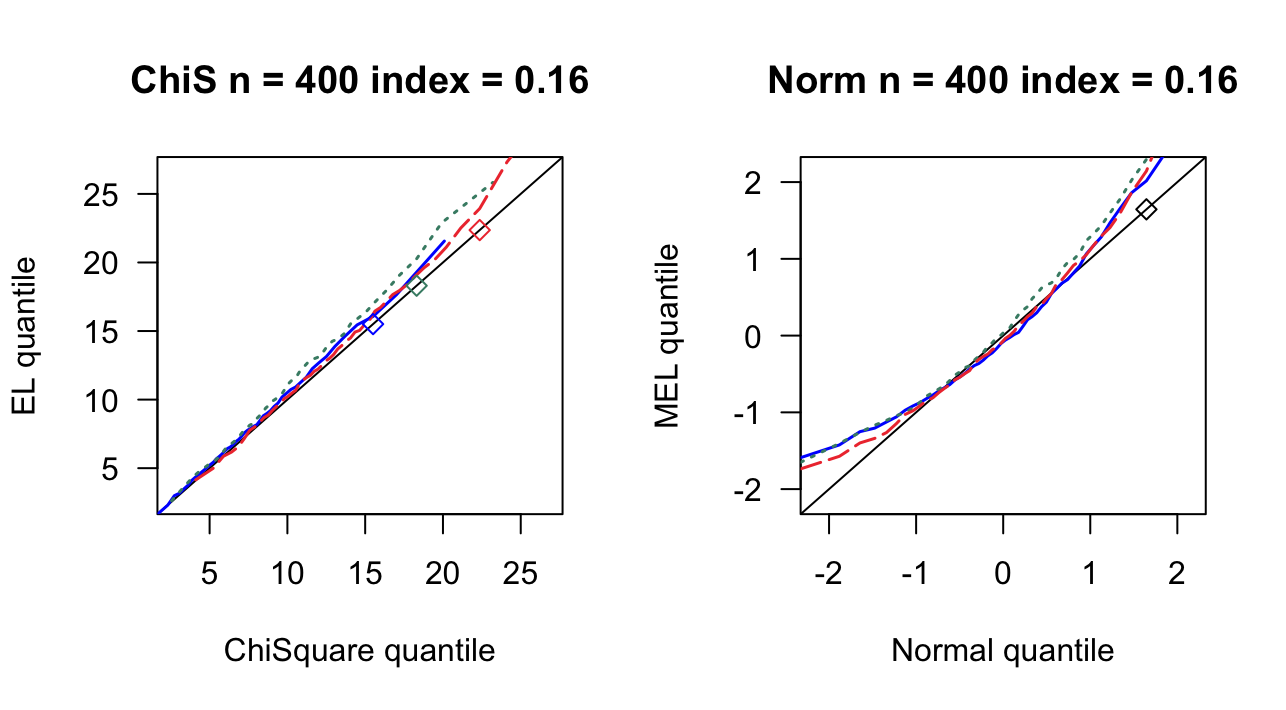
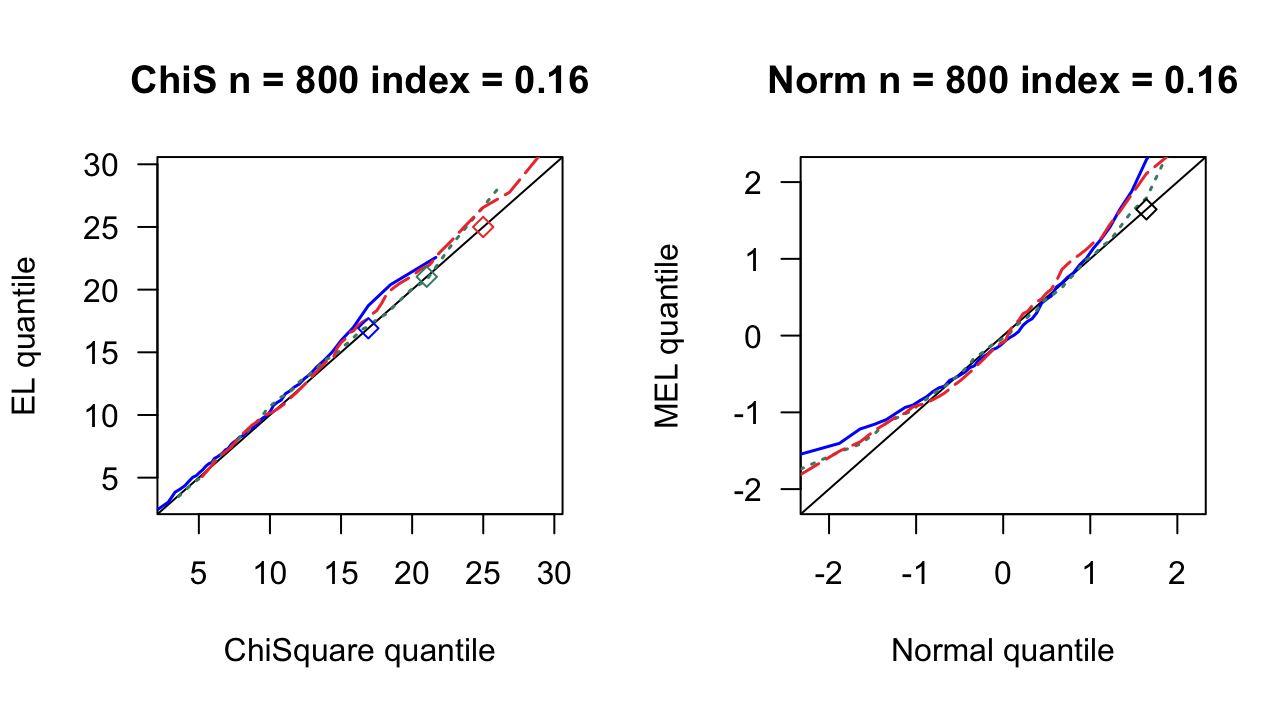
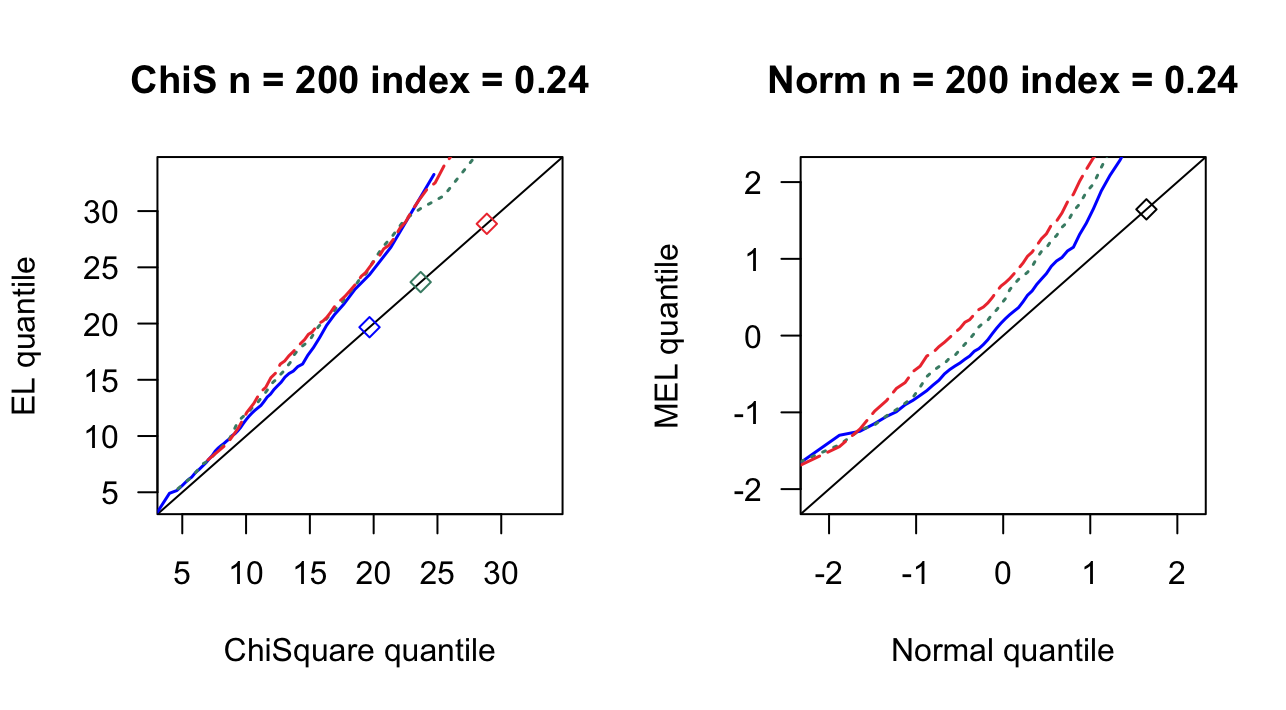
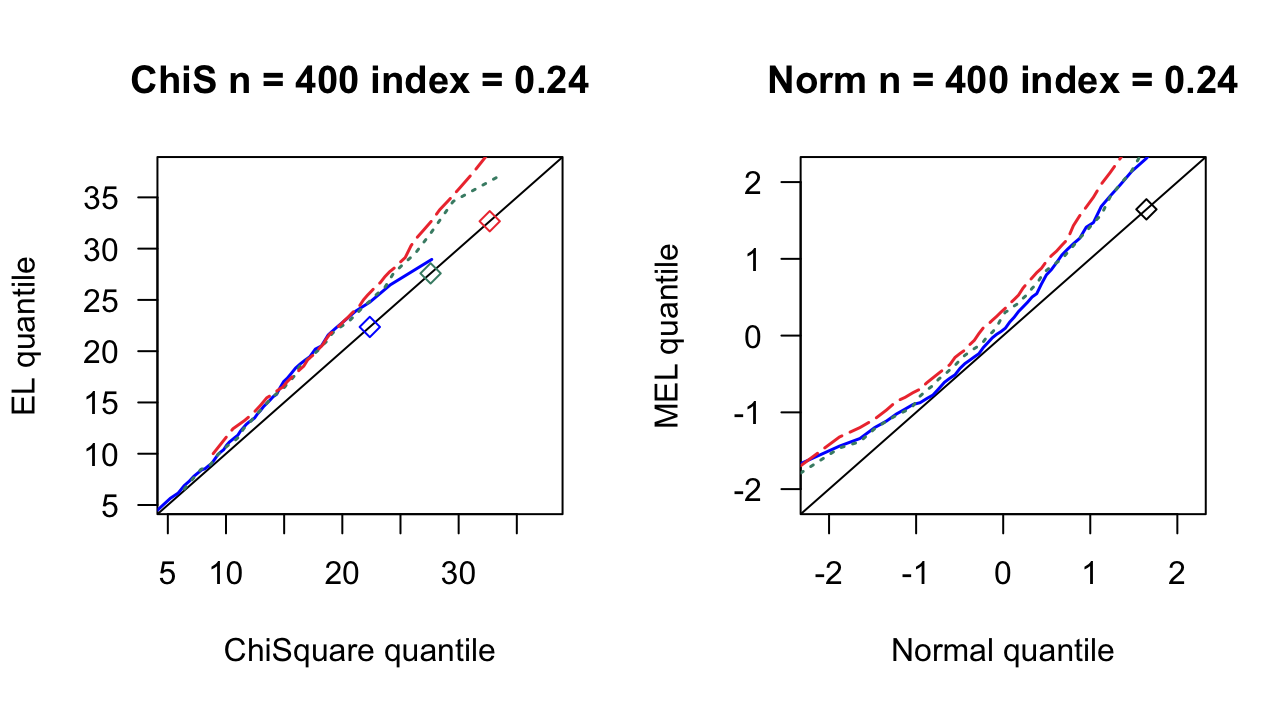
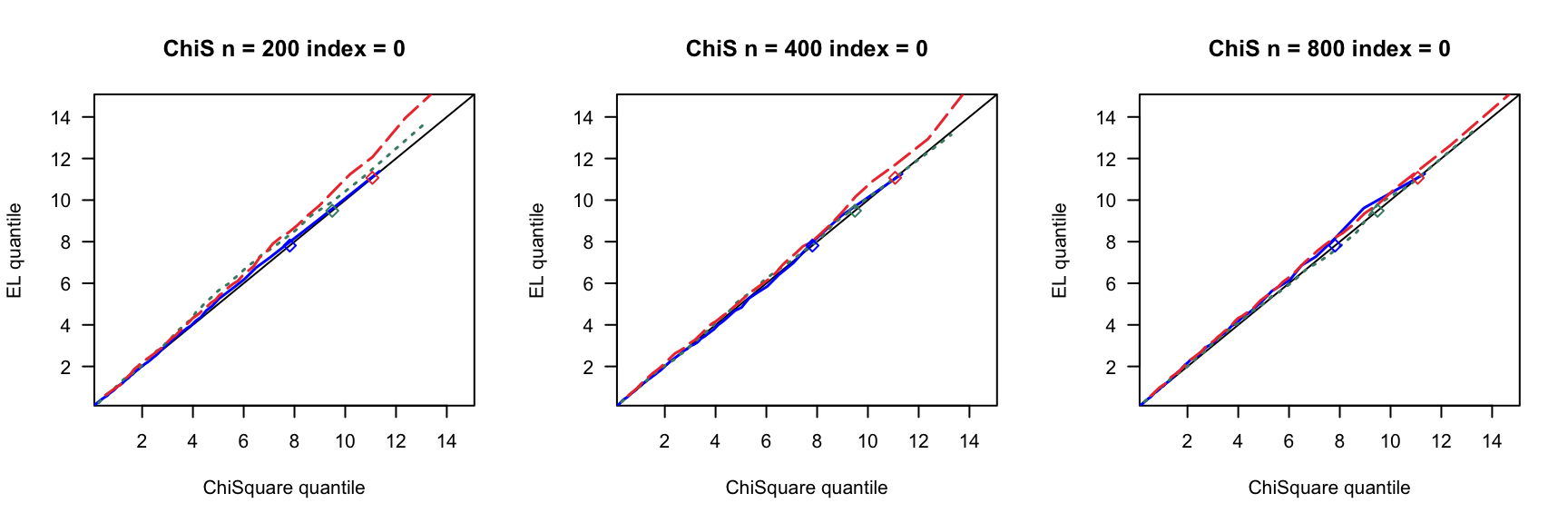
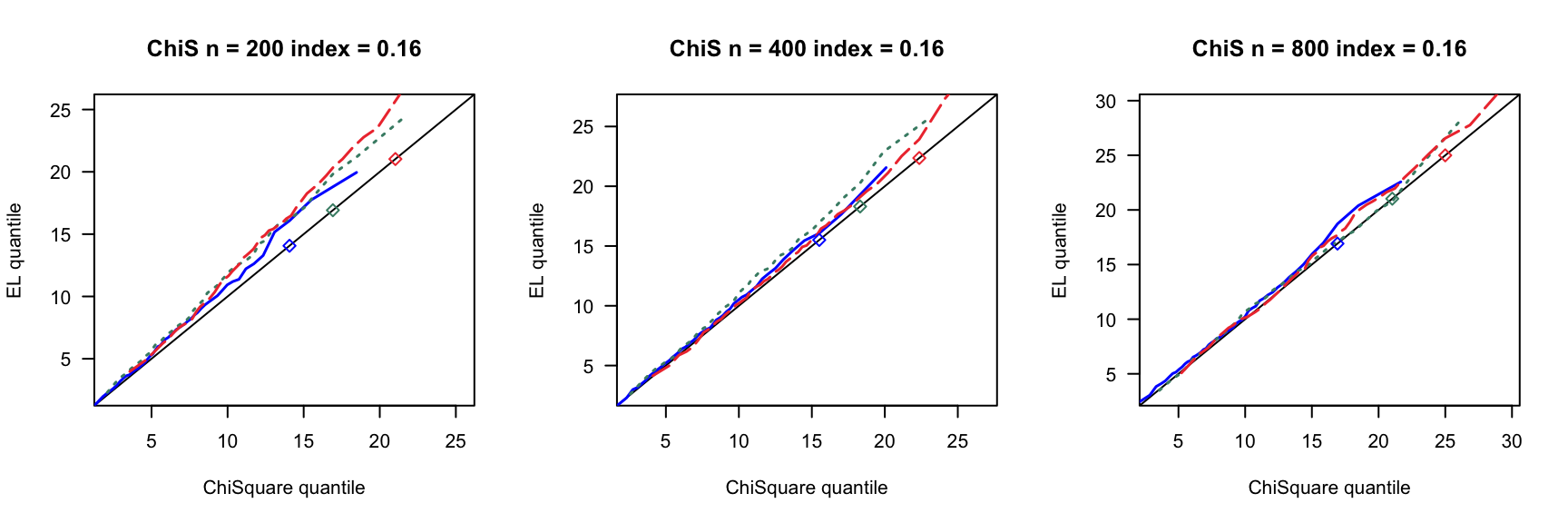
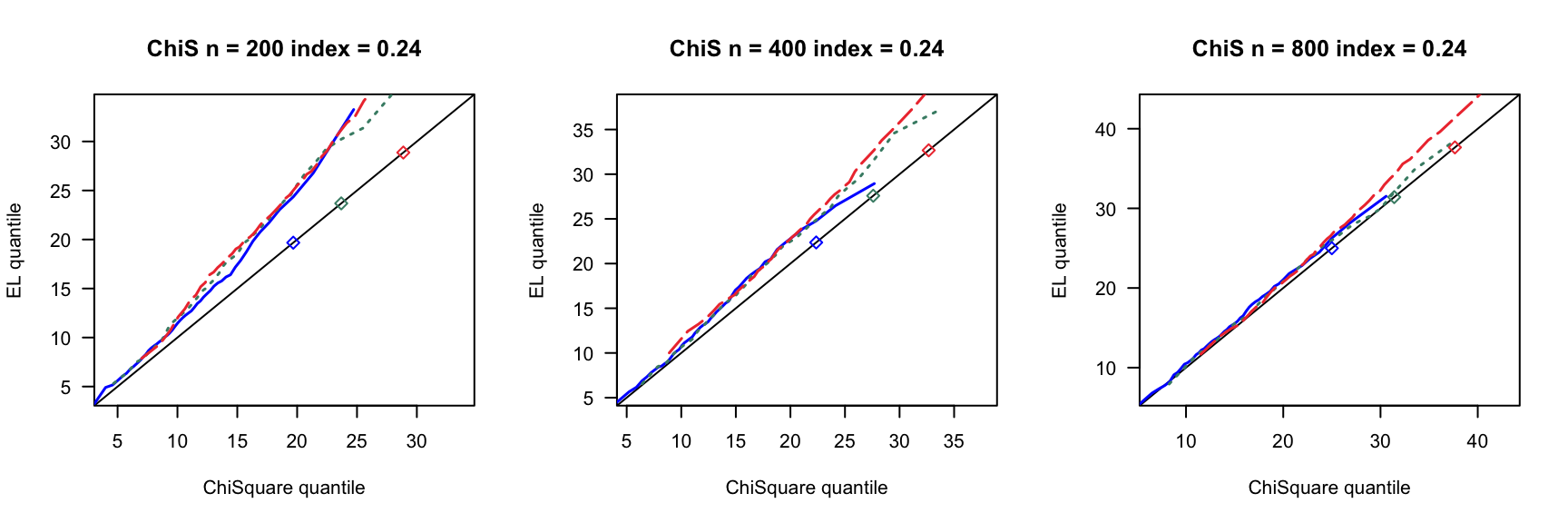
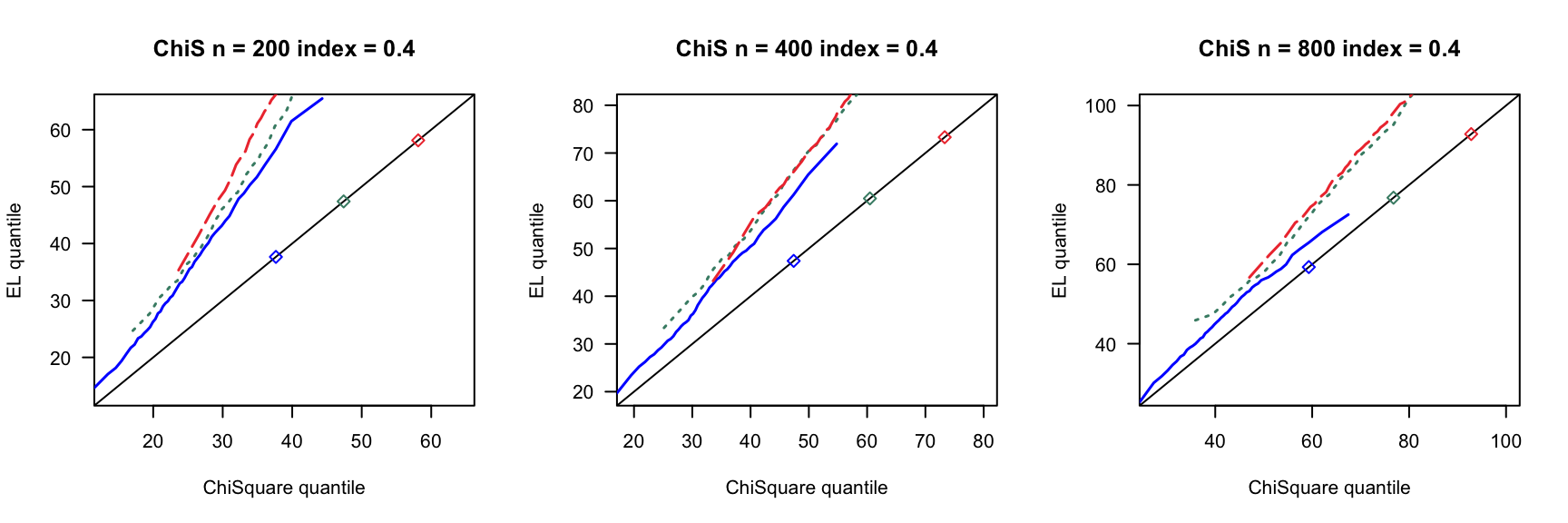
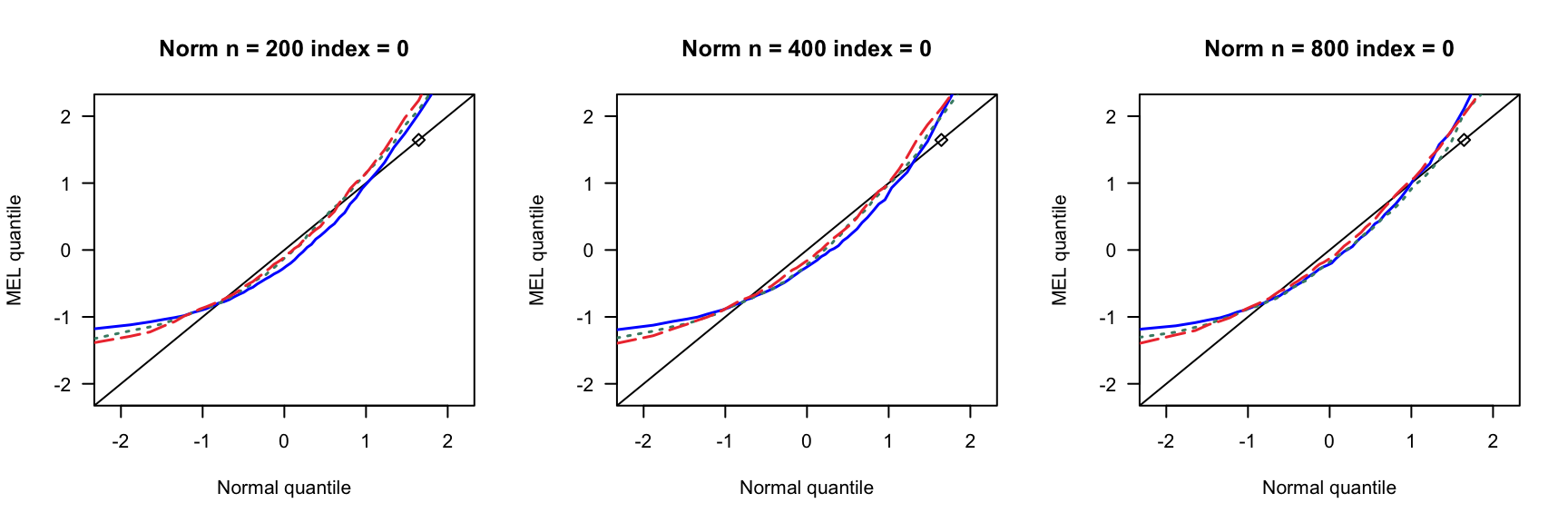
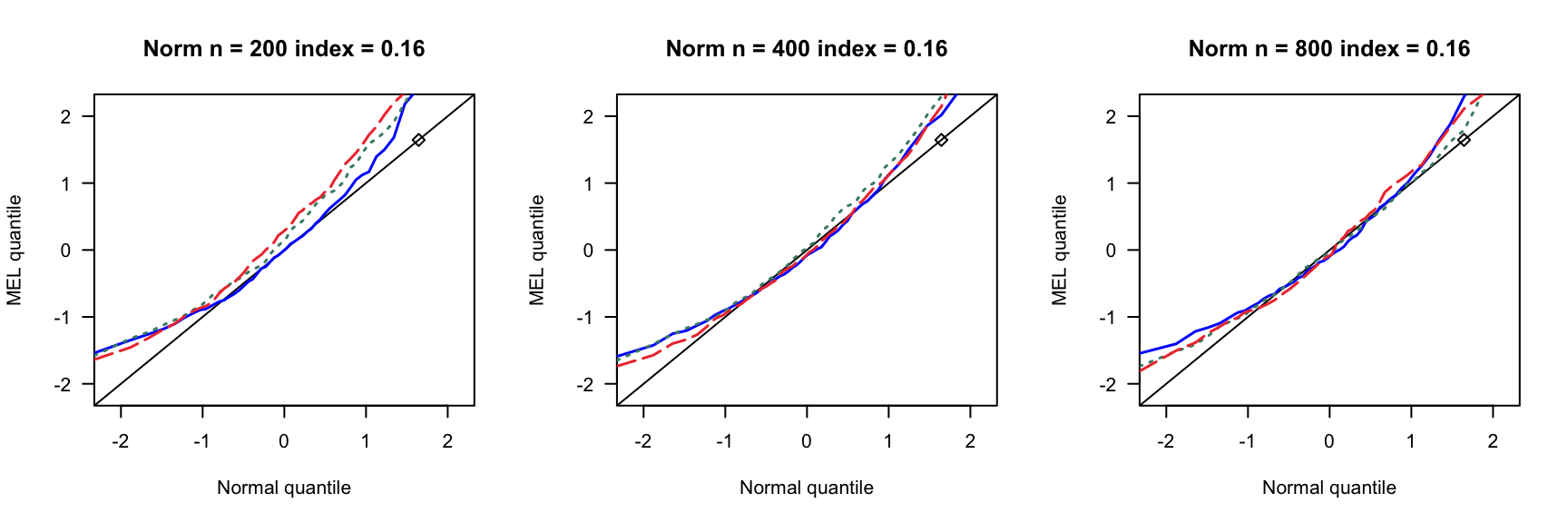
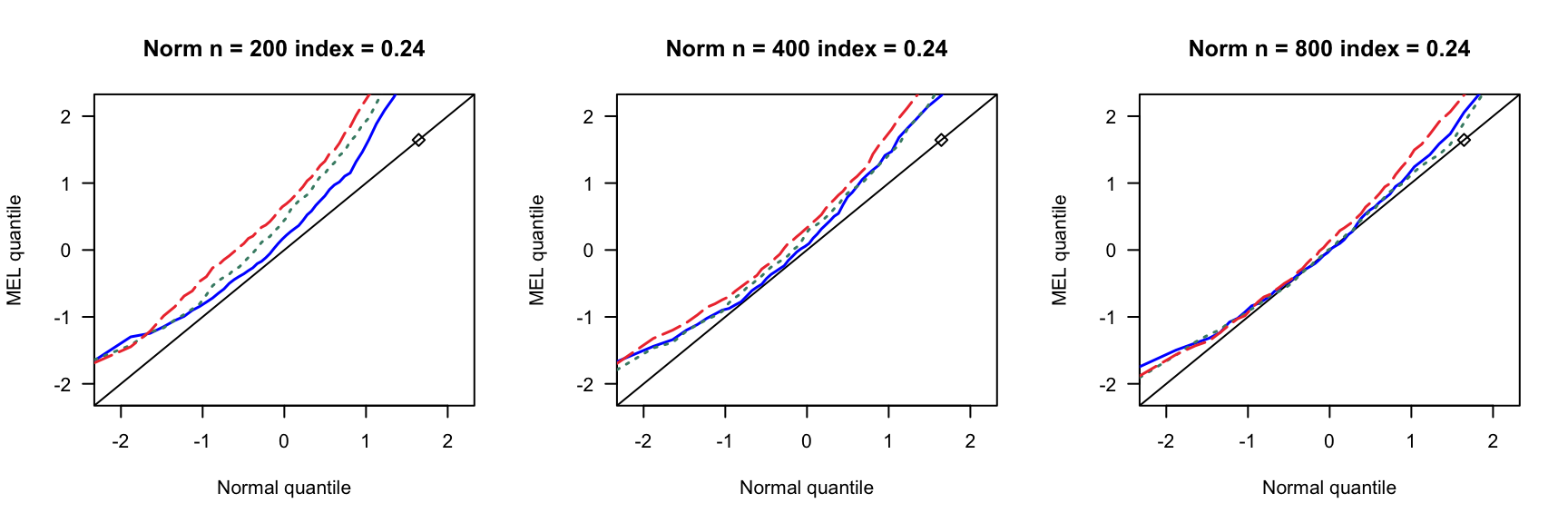
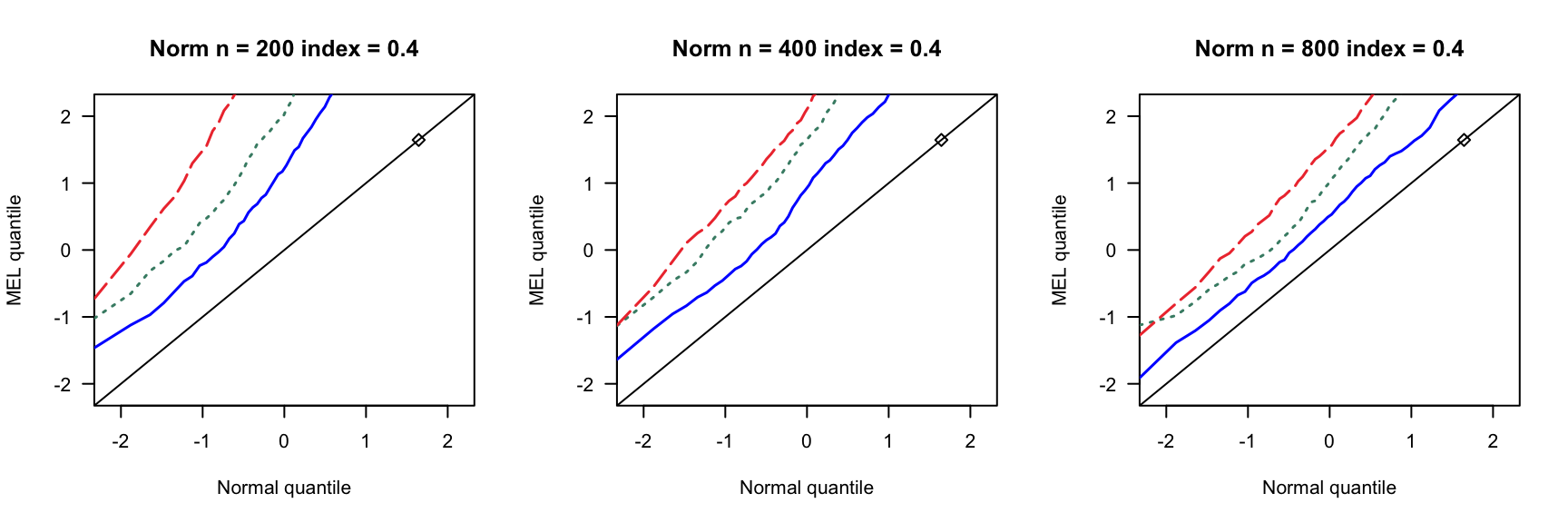
第 3 章 一般线性模型

根据2007ShiJian思想，参考QinYongsong给出的计算框架，做一个高维线性模型的模拟，其中$X_{ij}$的取值参考2020ChangJY第13页。相关代码见此。

$$Y = X^\mathsf{T}\beta + \epsilon$$

• $n$表示样本个数

  • $n = 200,400,800$

• $p$表示样本维数

  • $p=cn^{index}$
  • $index=0,0.16,0.24,0.4$
  • $c = 3,4,5$

• $X_i \sim N(0,\Sigma_{p}), \Sigma_{p}=(\sigma_{ij})_{p \times p}$

  • $\sigma_{ij}=I(i=j)+0.5I(i \neq j)$

  • $I(x \in \omega)= \left\{ \begin{aligned} \nonumber 1,& x \in \omega,\\ 0,&x \notin \omega.\\ \end{aligned} \right.$

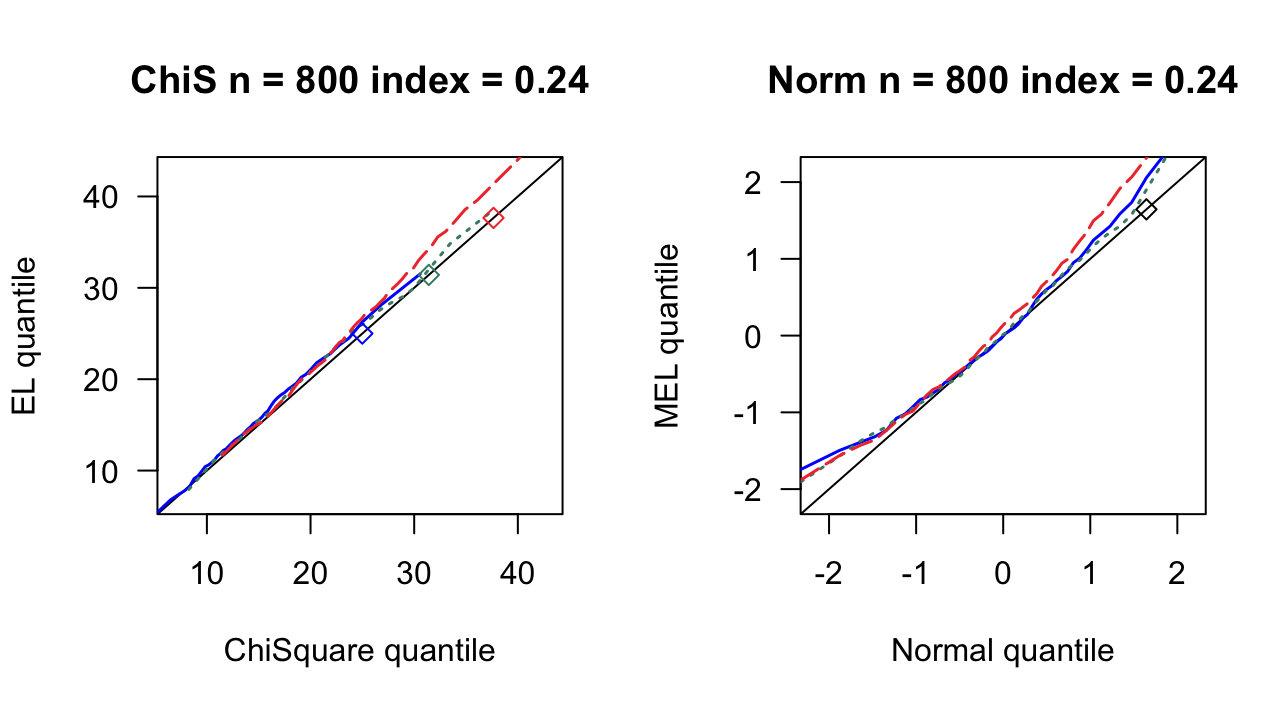
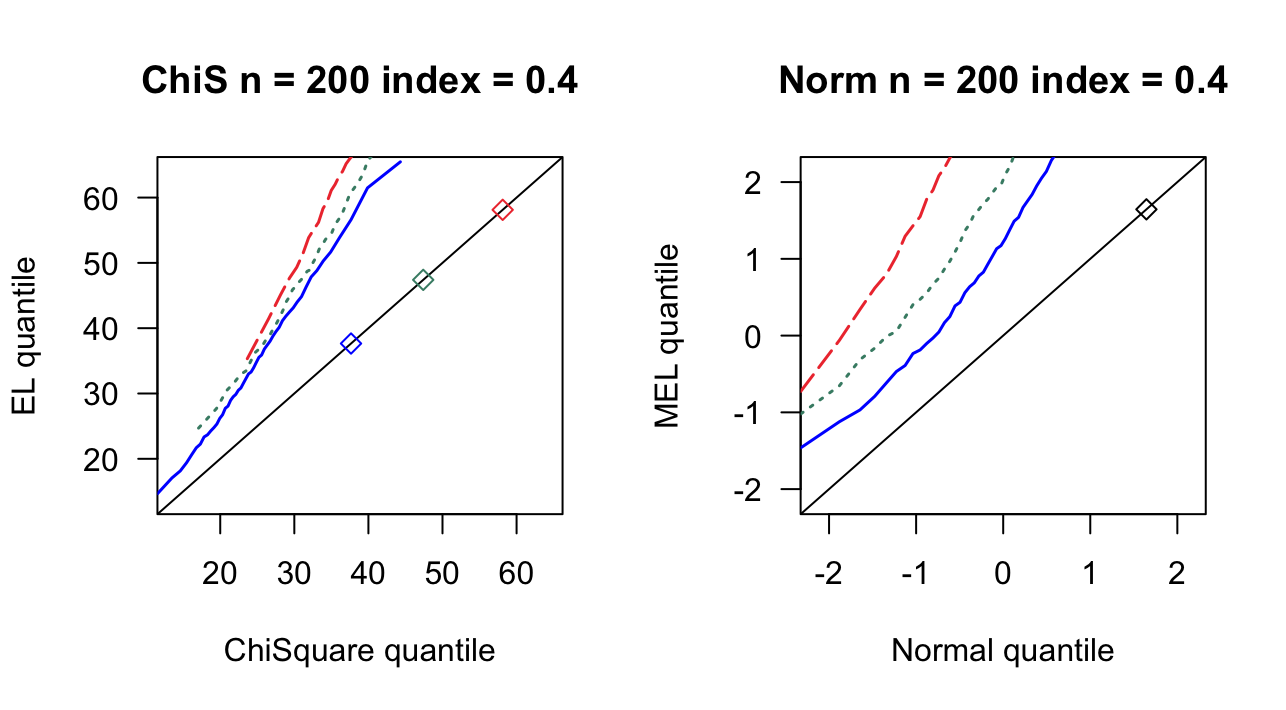
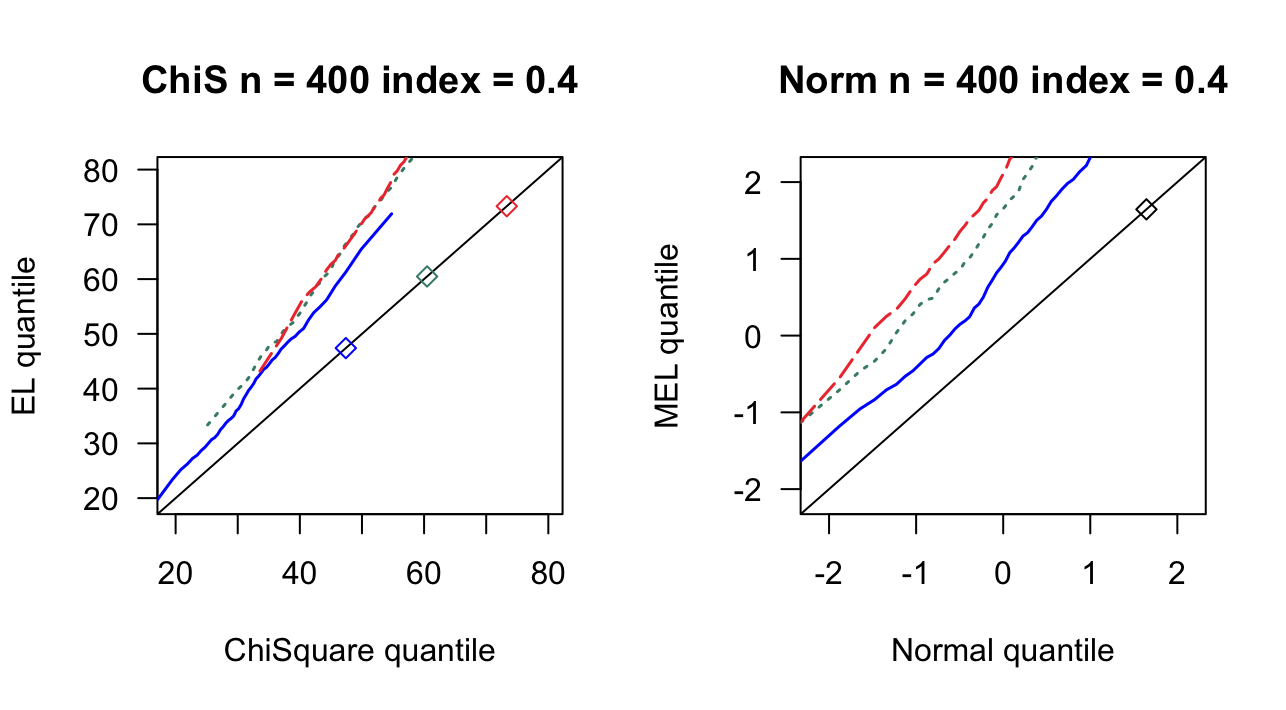
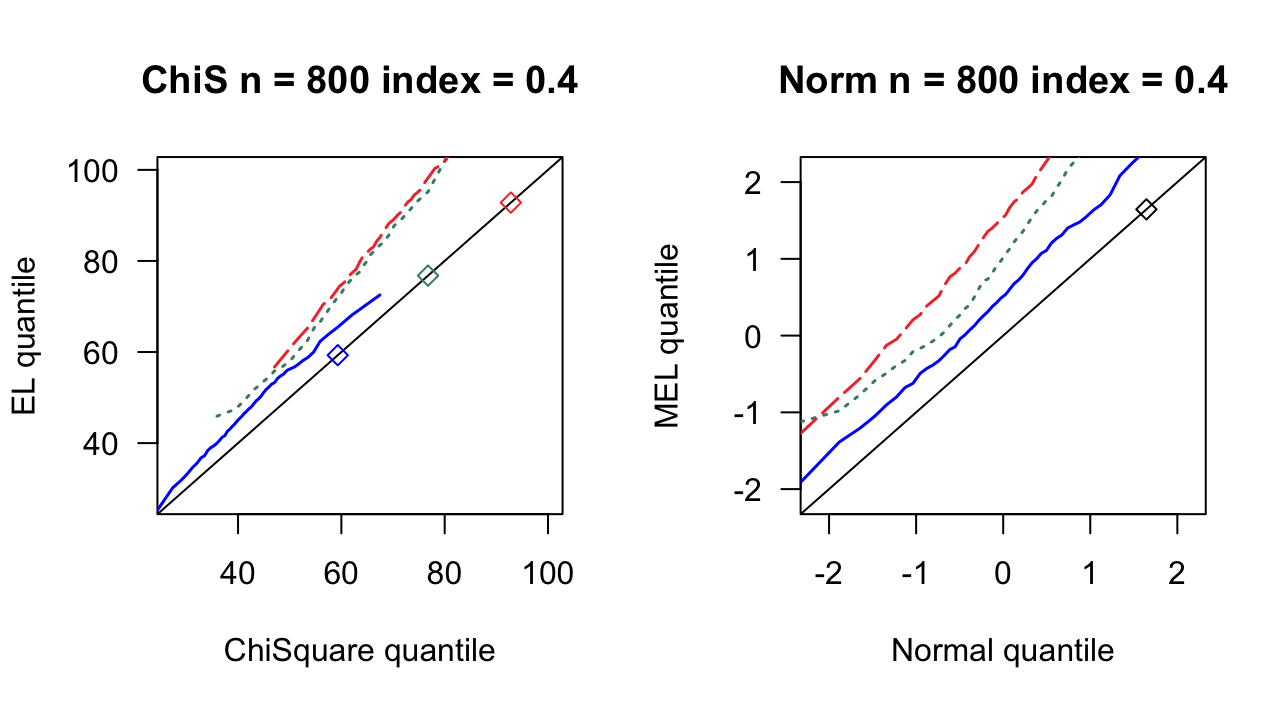
3.1 覆盖率

	n = 200			n = 400			n = 800
	p	EL	MEL	p	EL	MEL	p	EL	MEL
0	3	0.949	0.949	3	0.947	0.947	3	0.941	0.941
0	4	0.938	0.939	4	0.944	0.944	4	0.944	0.945
0	5	0.926	0.928	5	0.936	0.938	5	0.943	0.946
0.16	7	0.916	0.924	8	0.934	0.942	9	0.928	0.934
0.16	9	0.894	0.910	10	0.918	0.922	12	0.956	0.956
0.16	12	0.870	0.882	13	0.926	0.938	15	0.928	0.934
0.24	11	0.862	0.872	13	0.894	0.910	15	0.932	0.942
0.24	14	0.822	0.846	17	0.890	0.904	20	0.944	0.950
0.24	18	0.786	0.800	21	0.848	0.866	25	0.900	0.910
0.4	25	0.620	0.654	33	0.716	0.752	43	0.878	0.888
0.4	33	0.428	0.488	44	0.526	0.582	58	0.684	0.736
0.4	42	0.188	0.218	55	0.412	0.474	72	0.546	0.624

3.2 分位数图

3.3 EL 卡方

3.4 MEL 正态