第 5 章 其他误差SARAR

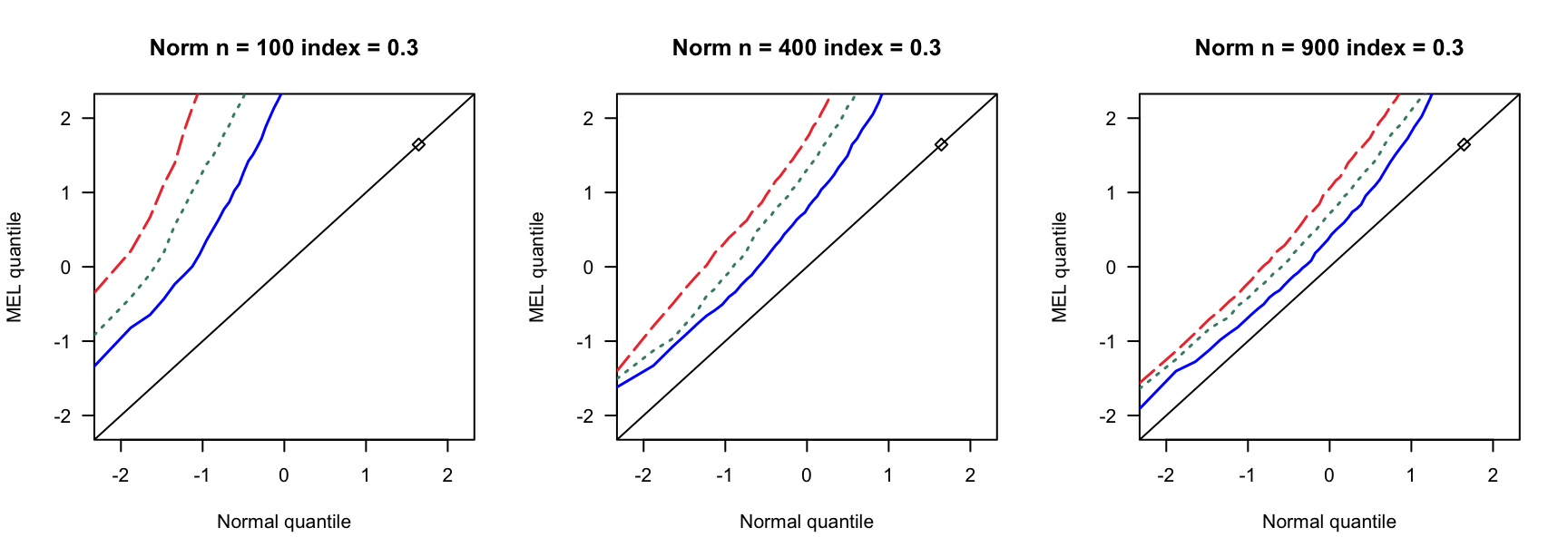
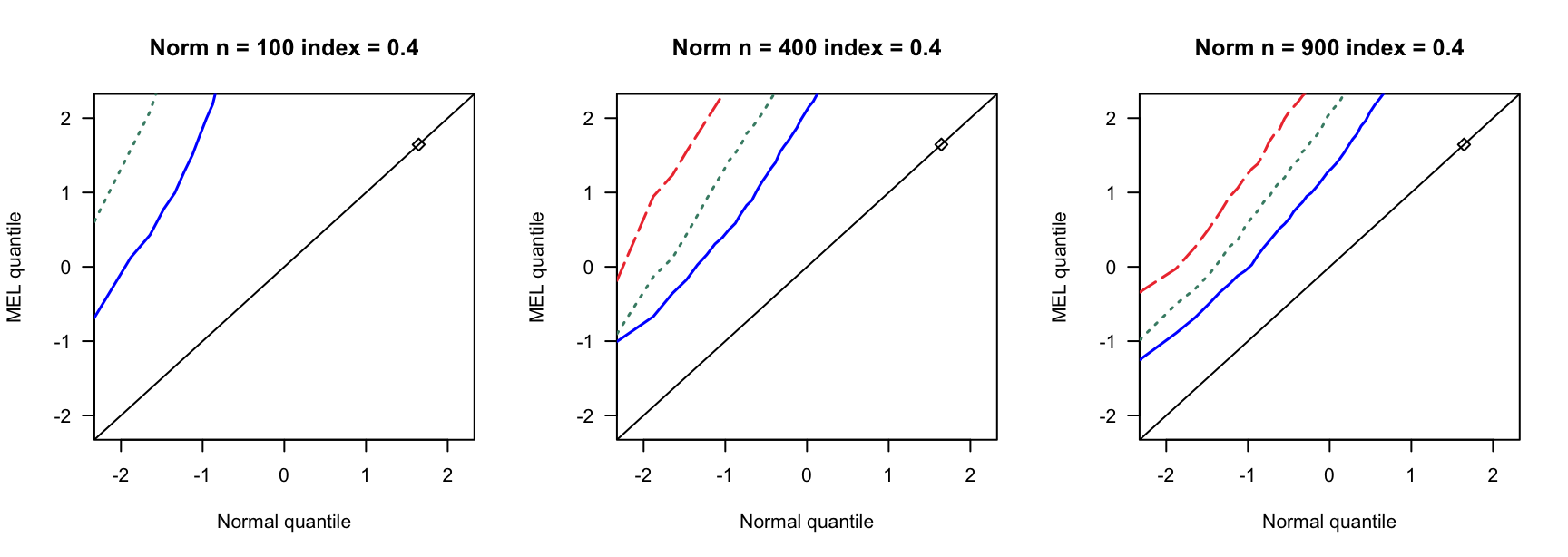
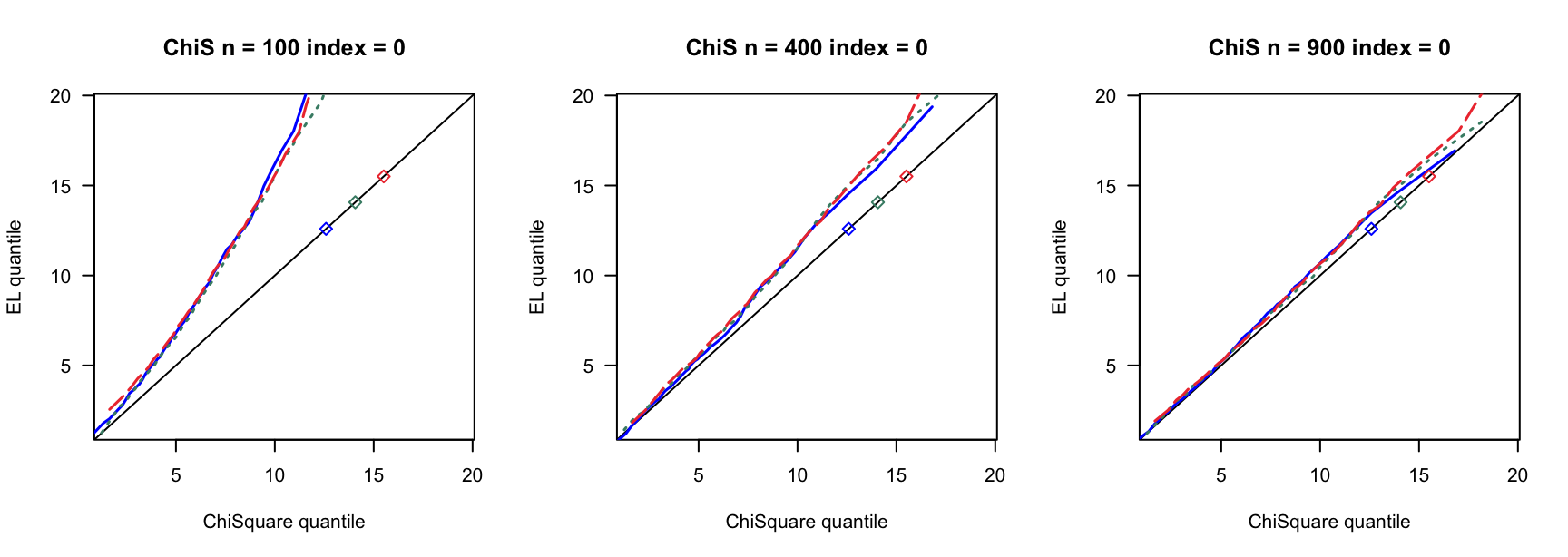
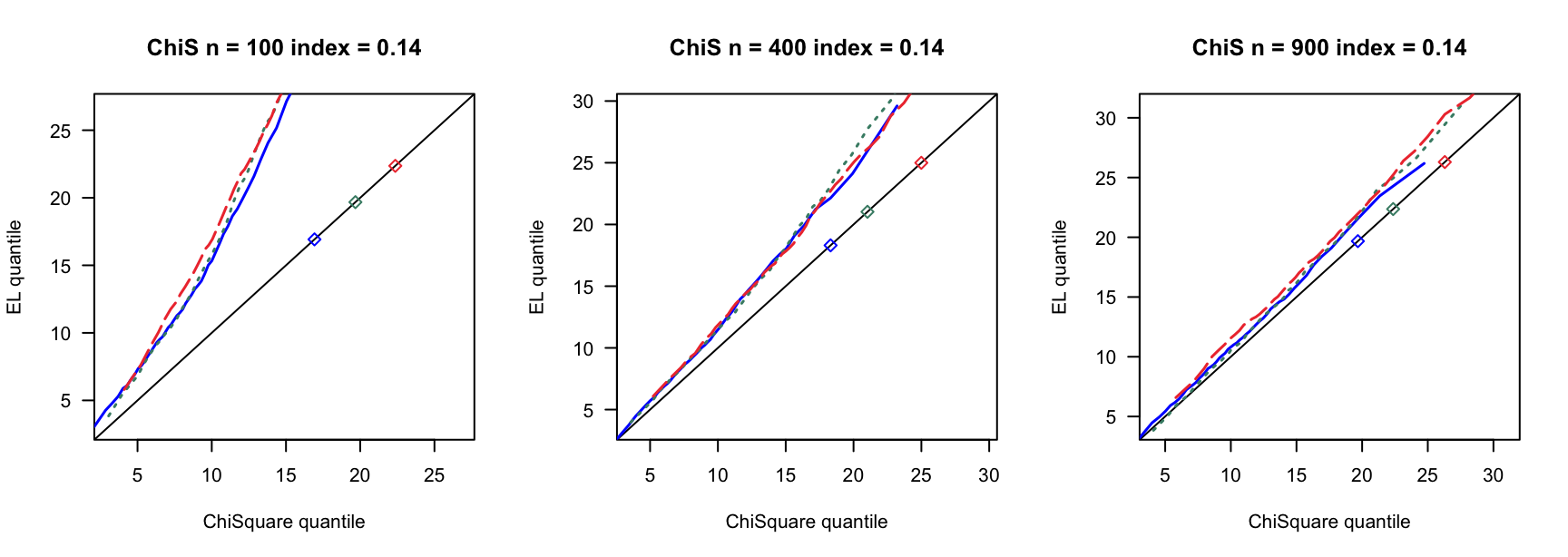
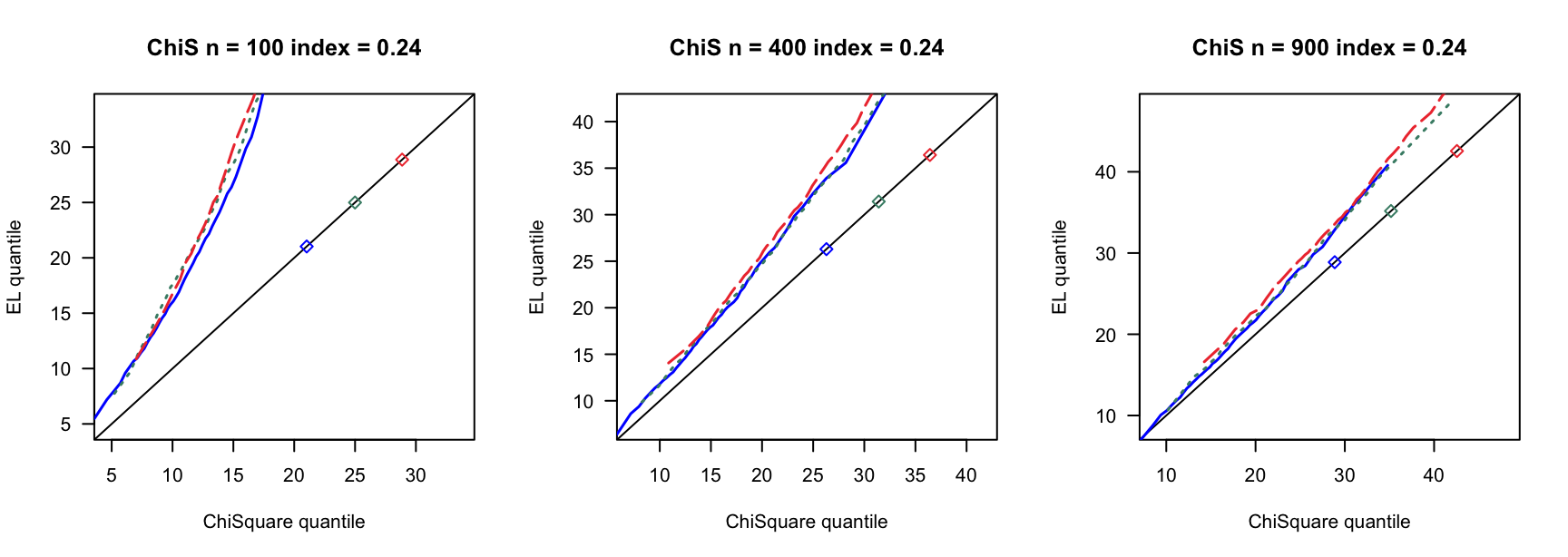
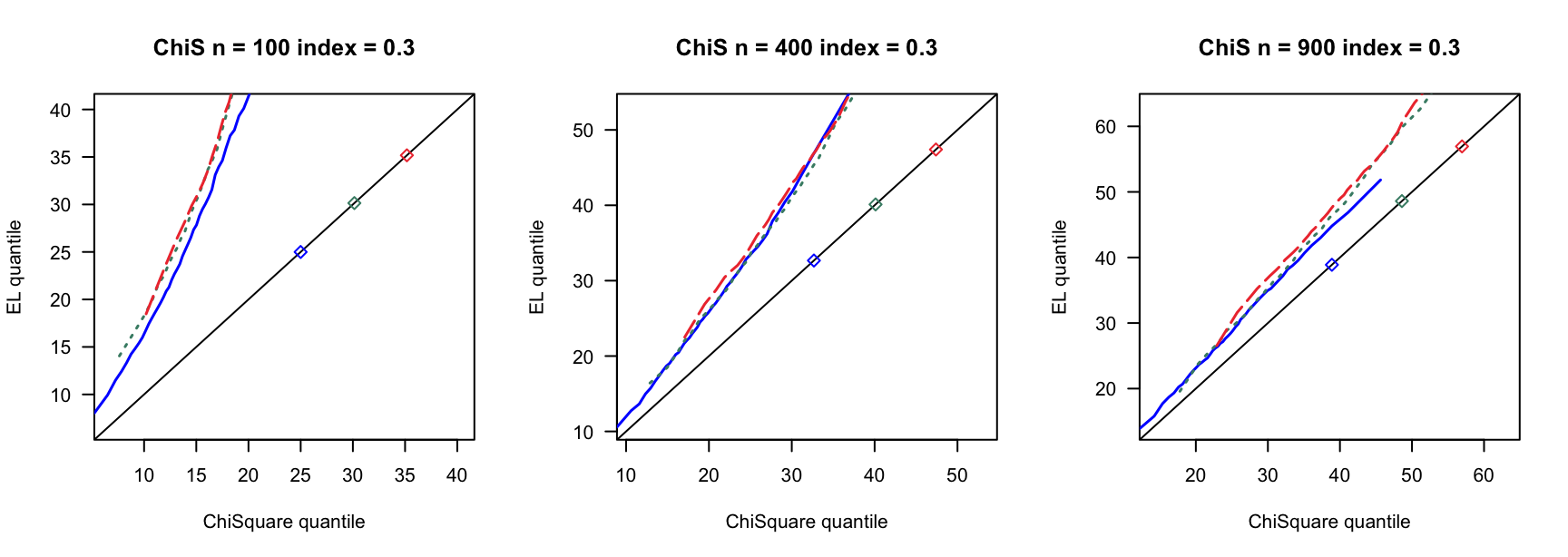
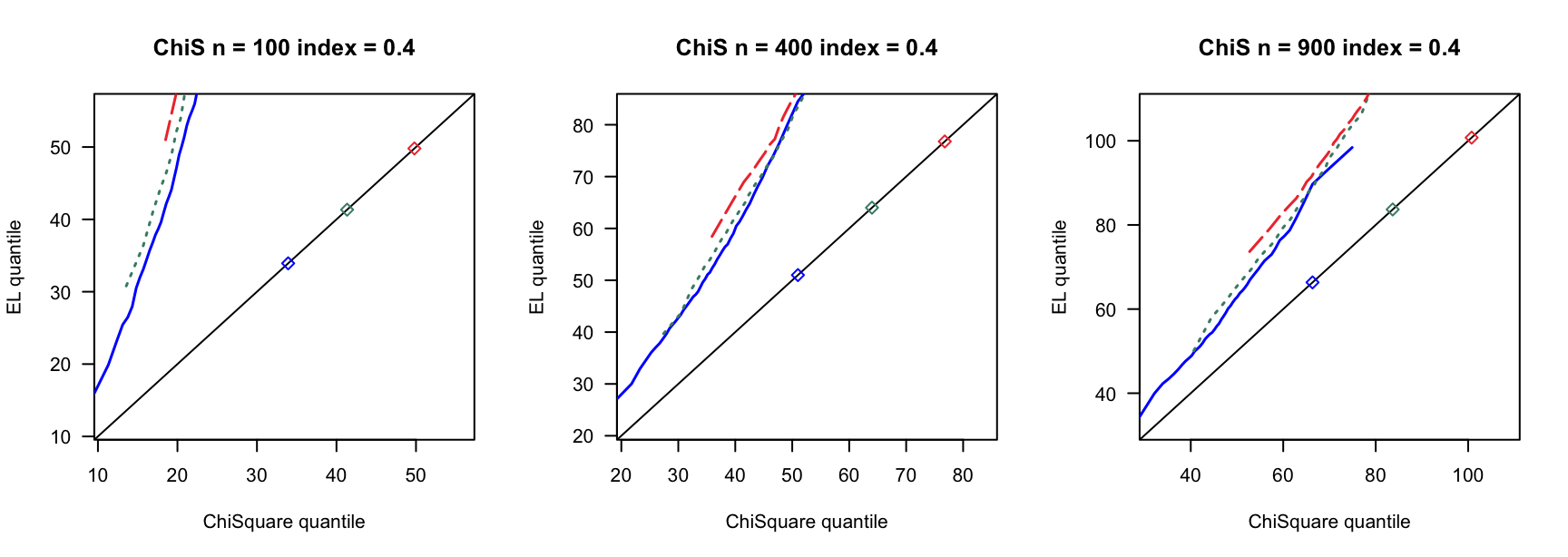
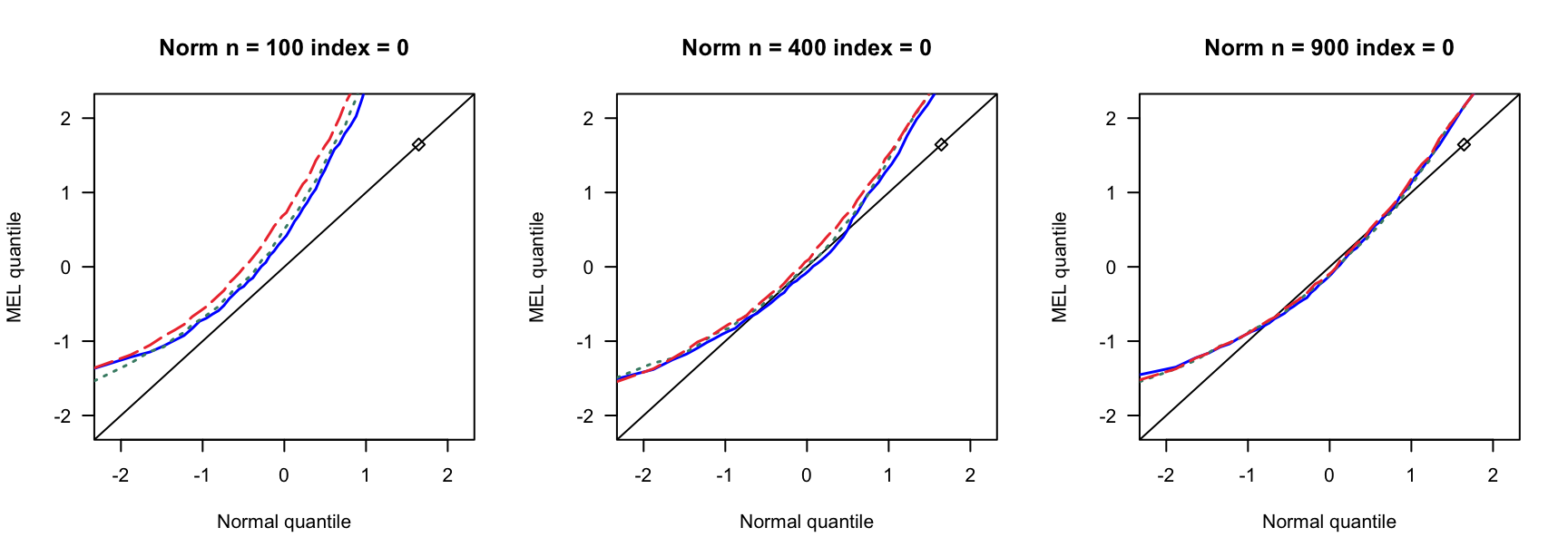
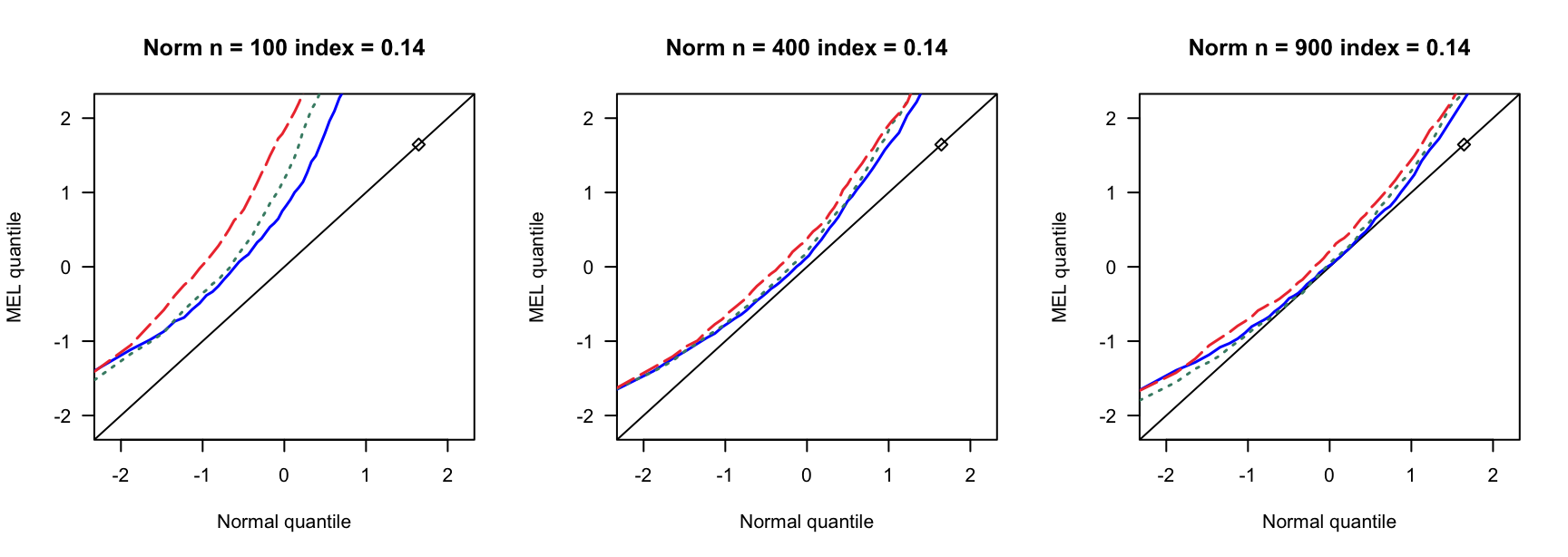
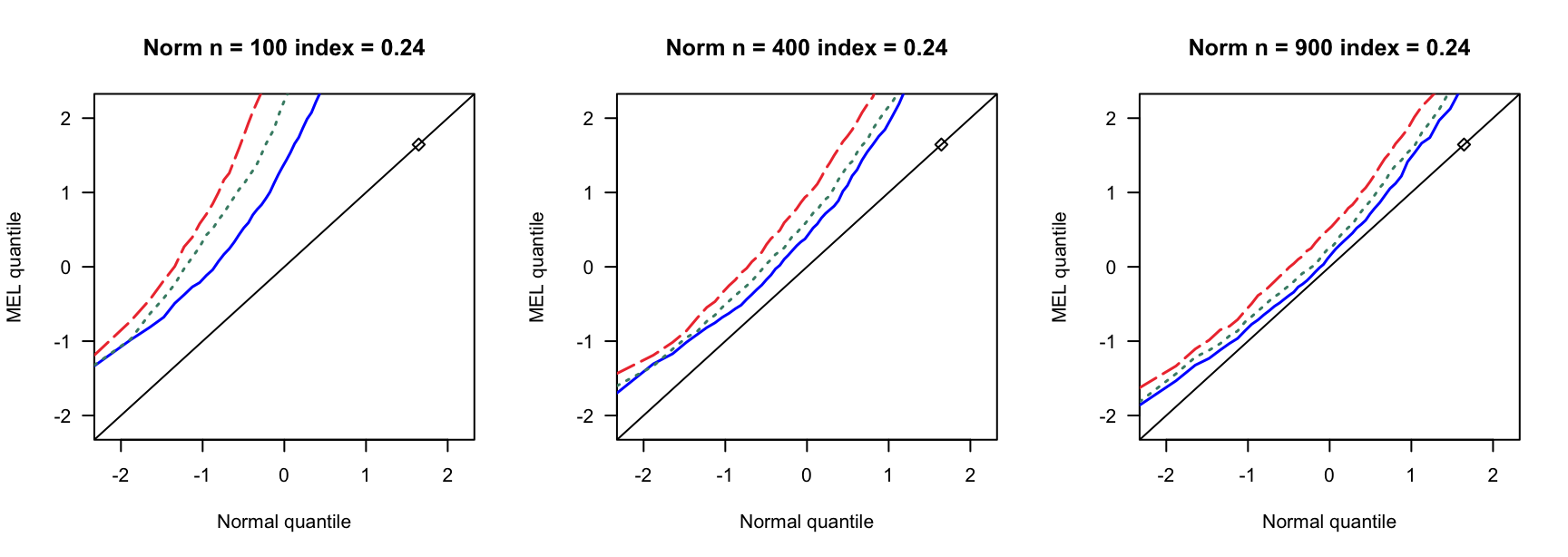
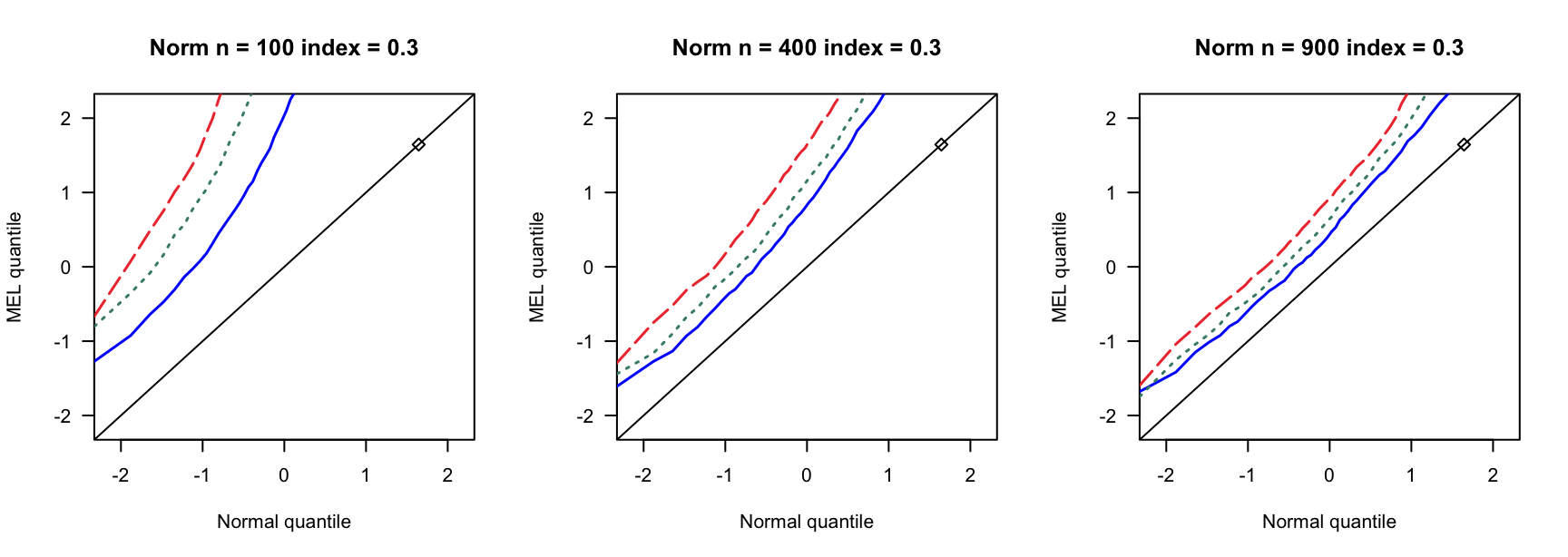
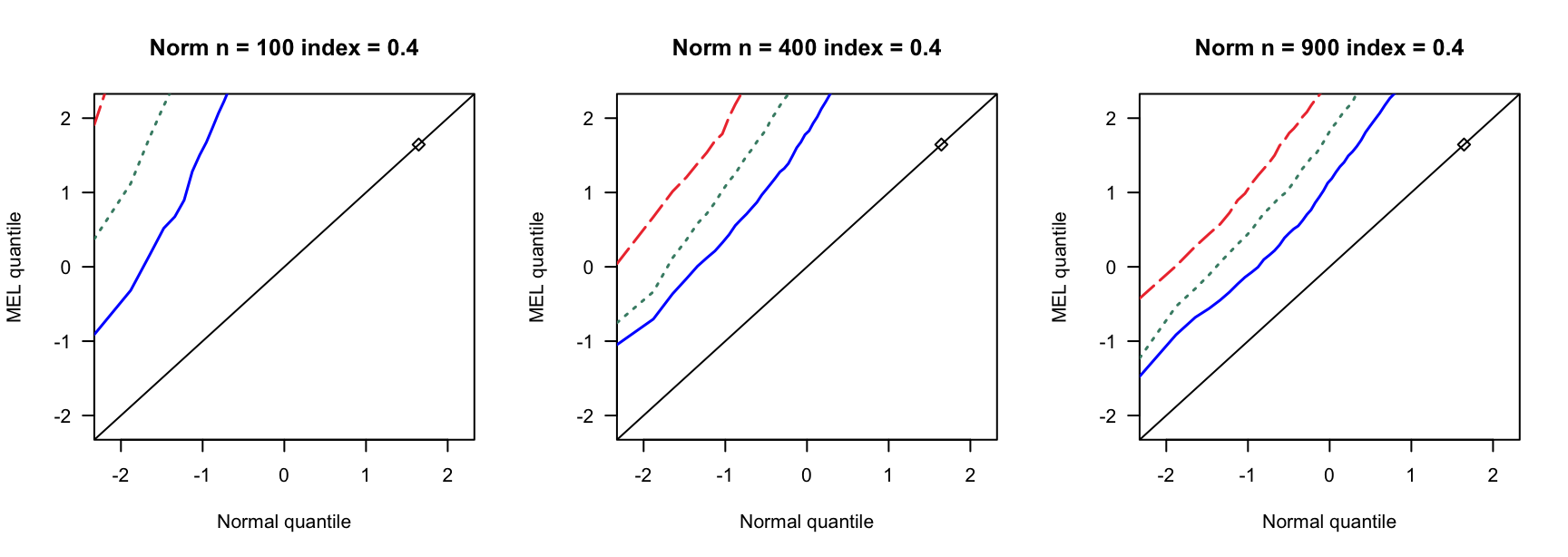
探究高维SARAR在不同误差分布下的表现。

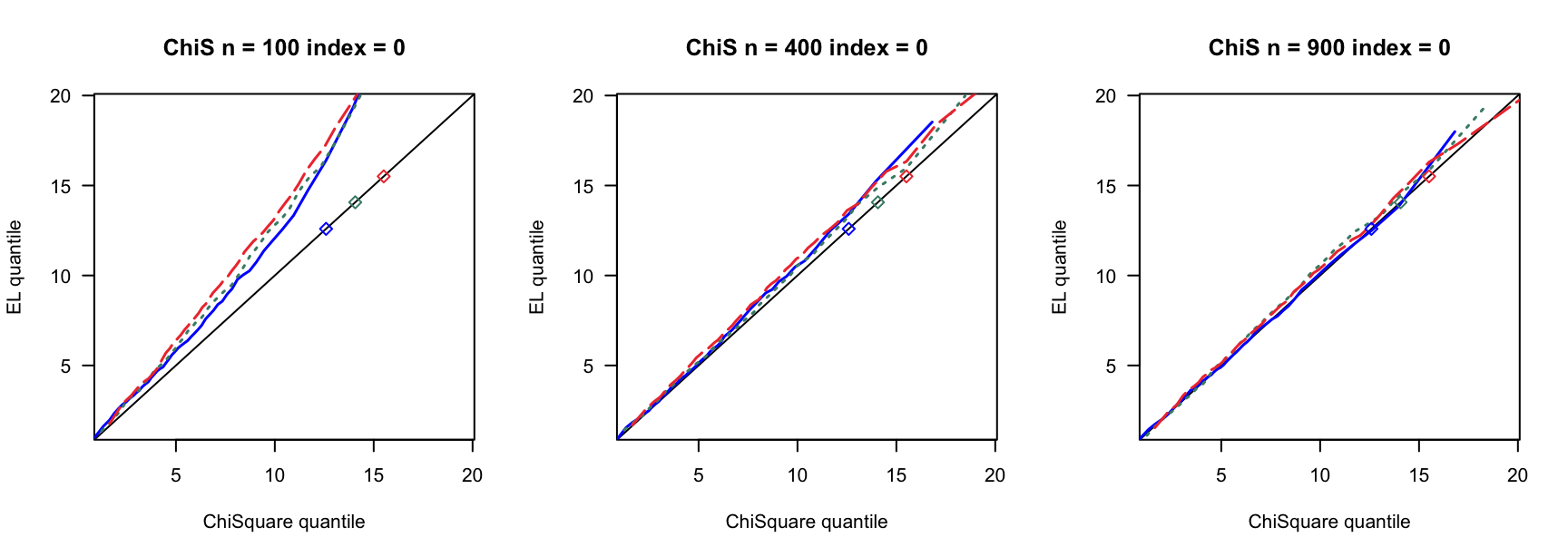
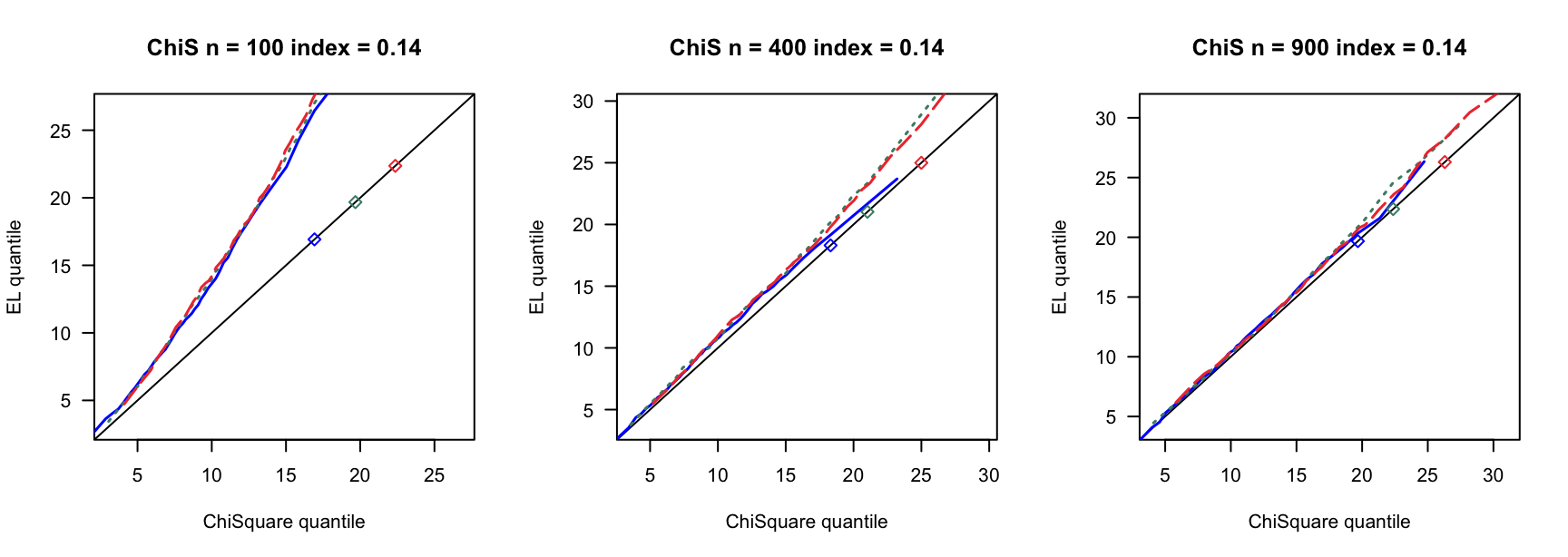
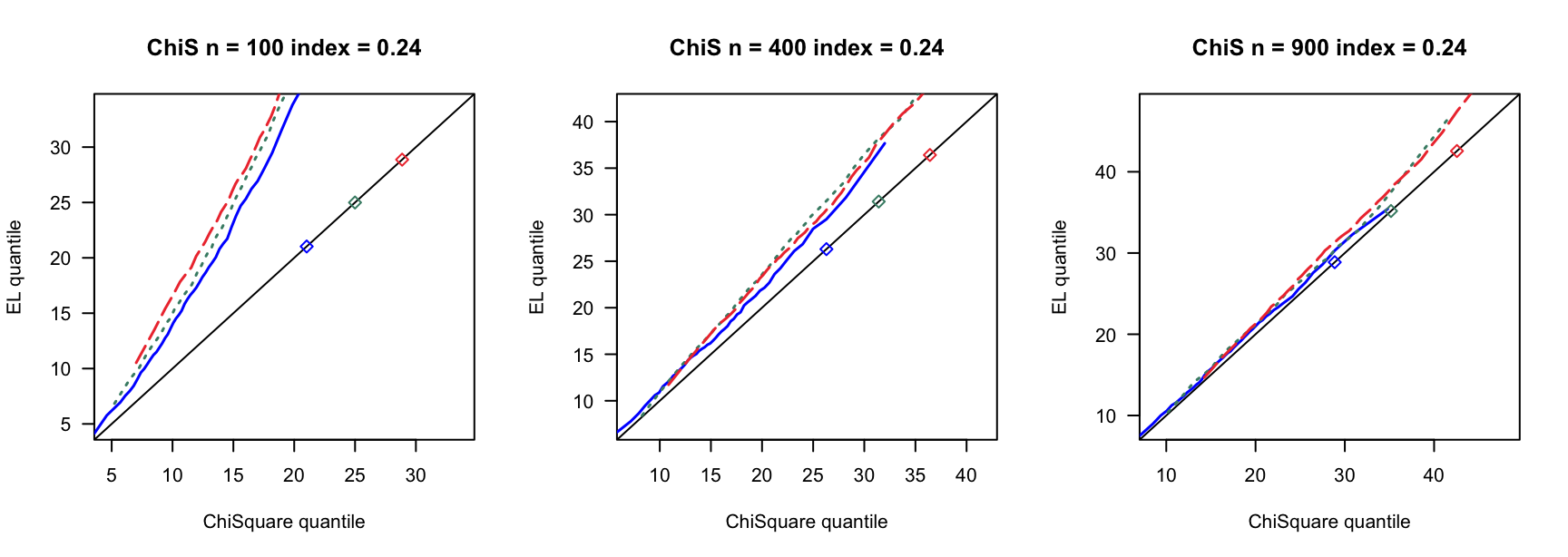
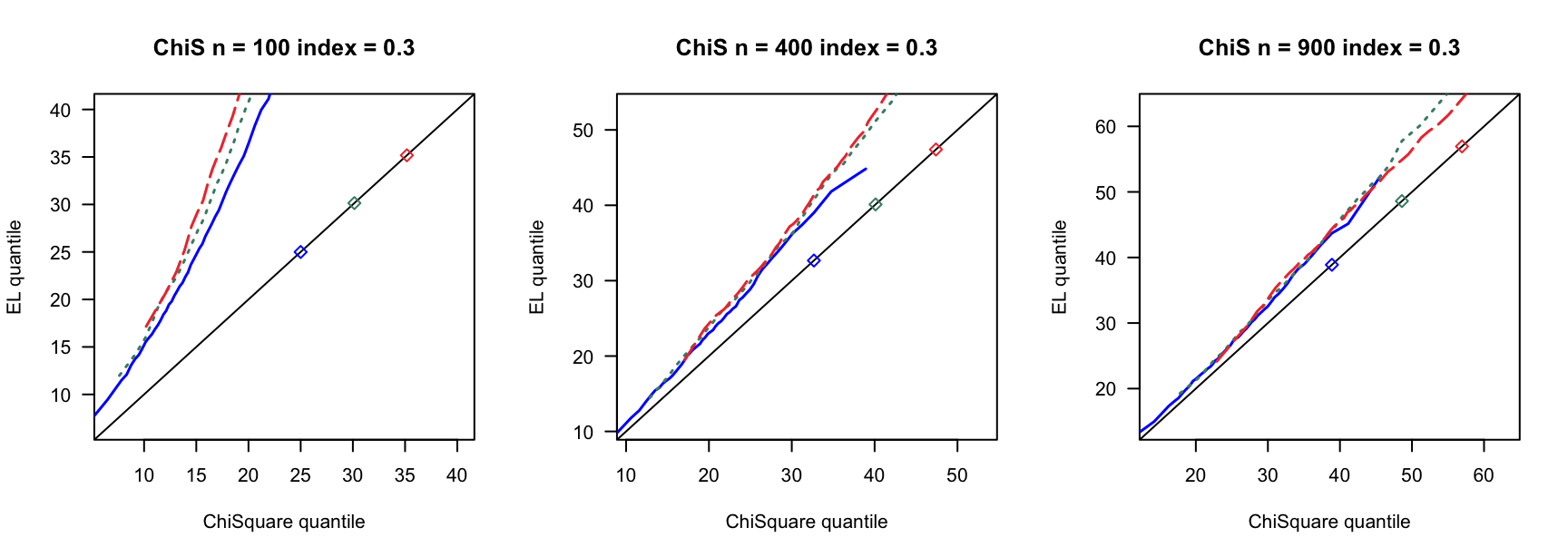
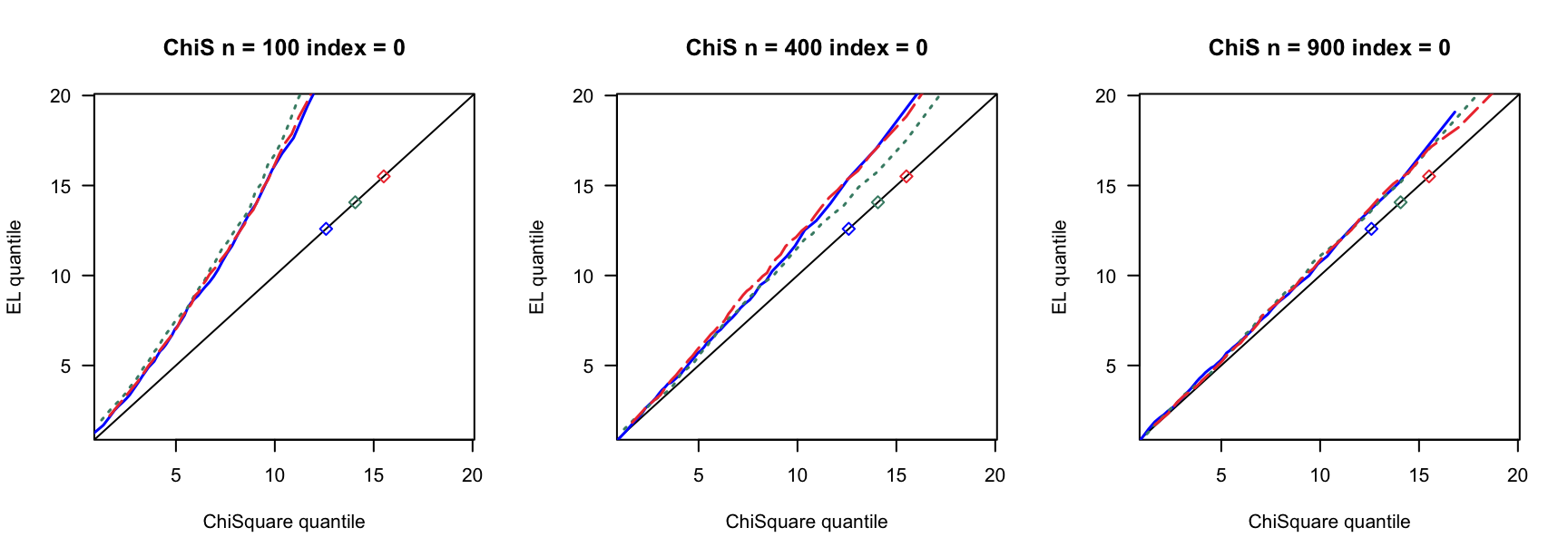
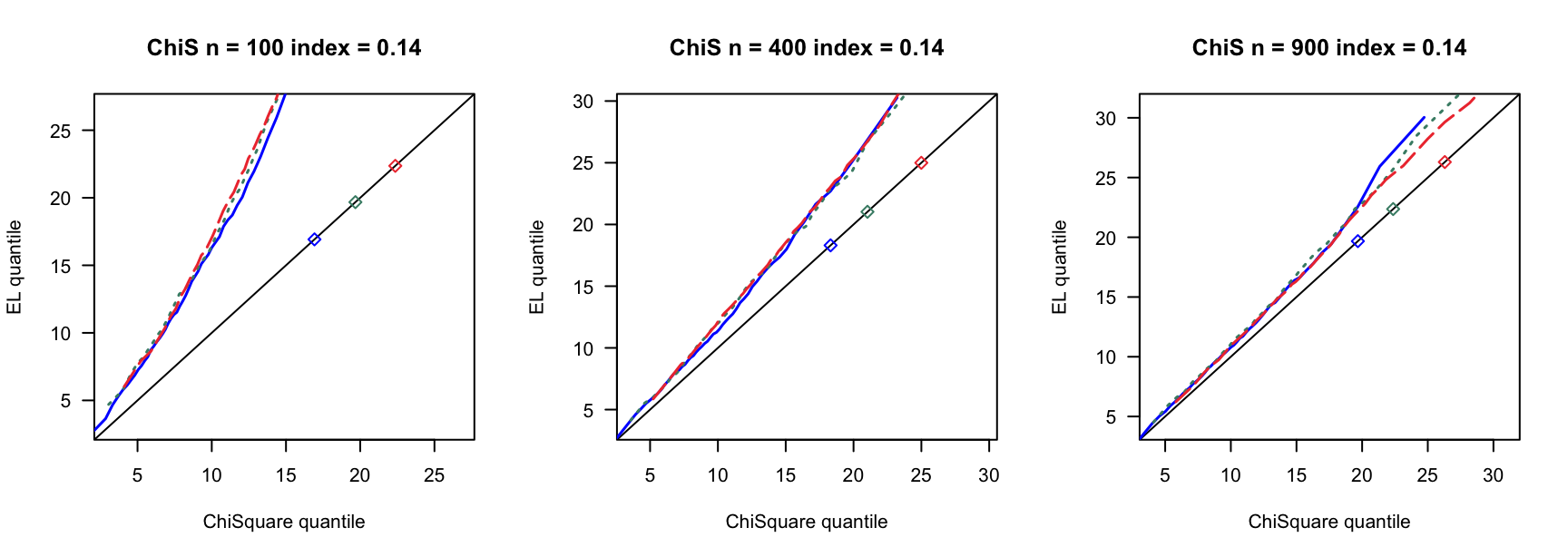
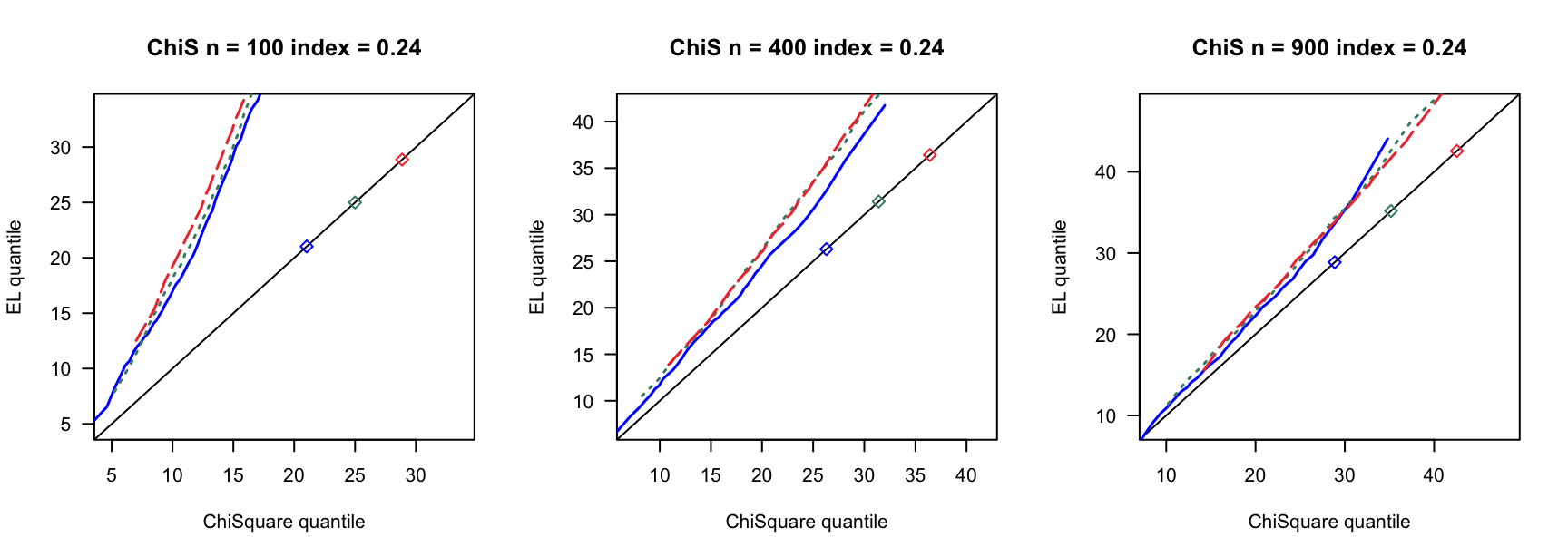
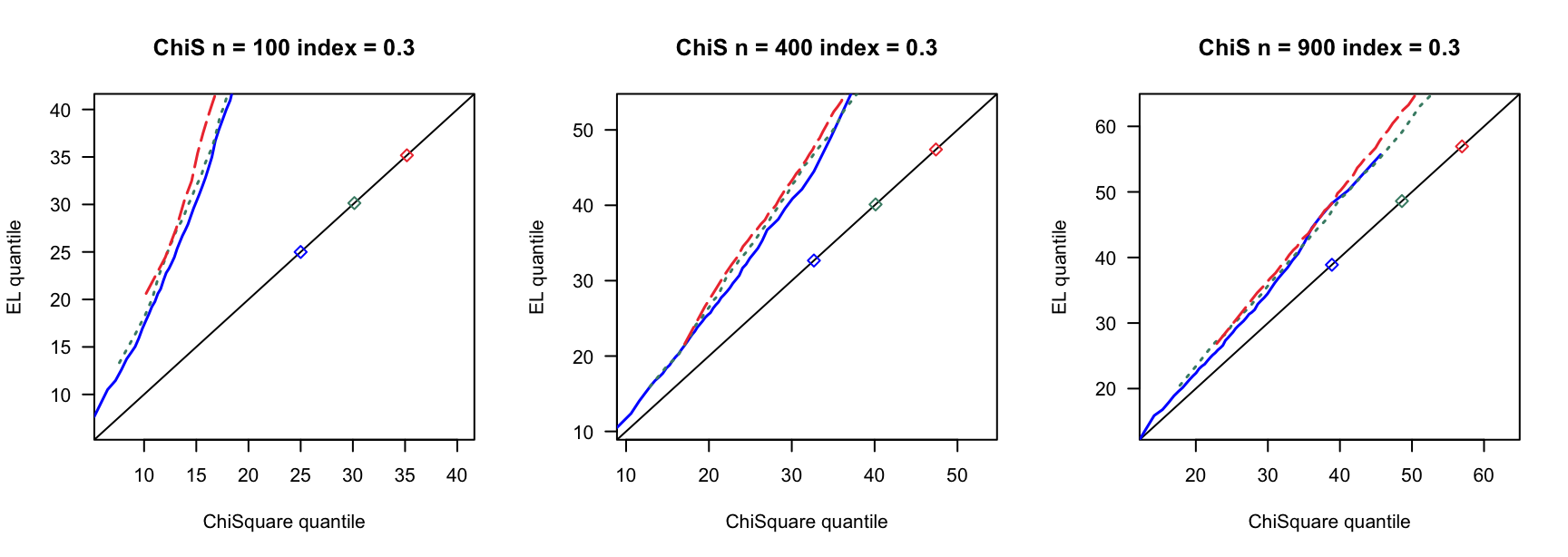
5.1 覆盖率

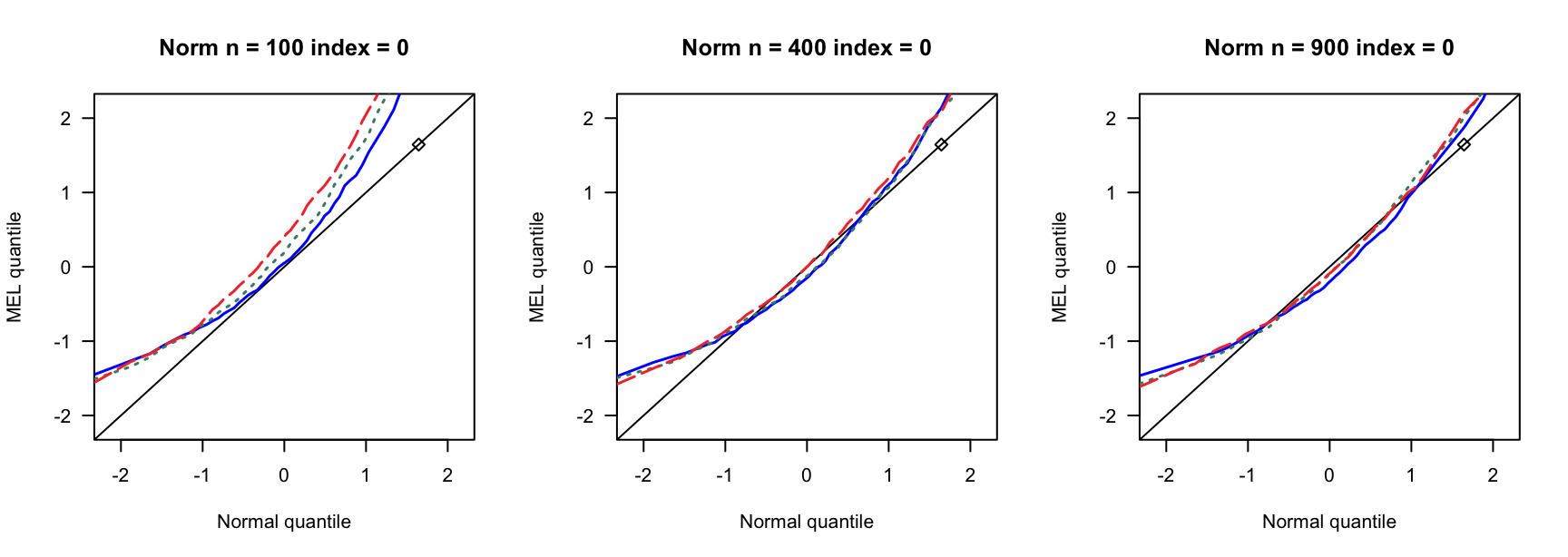
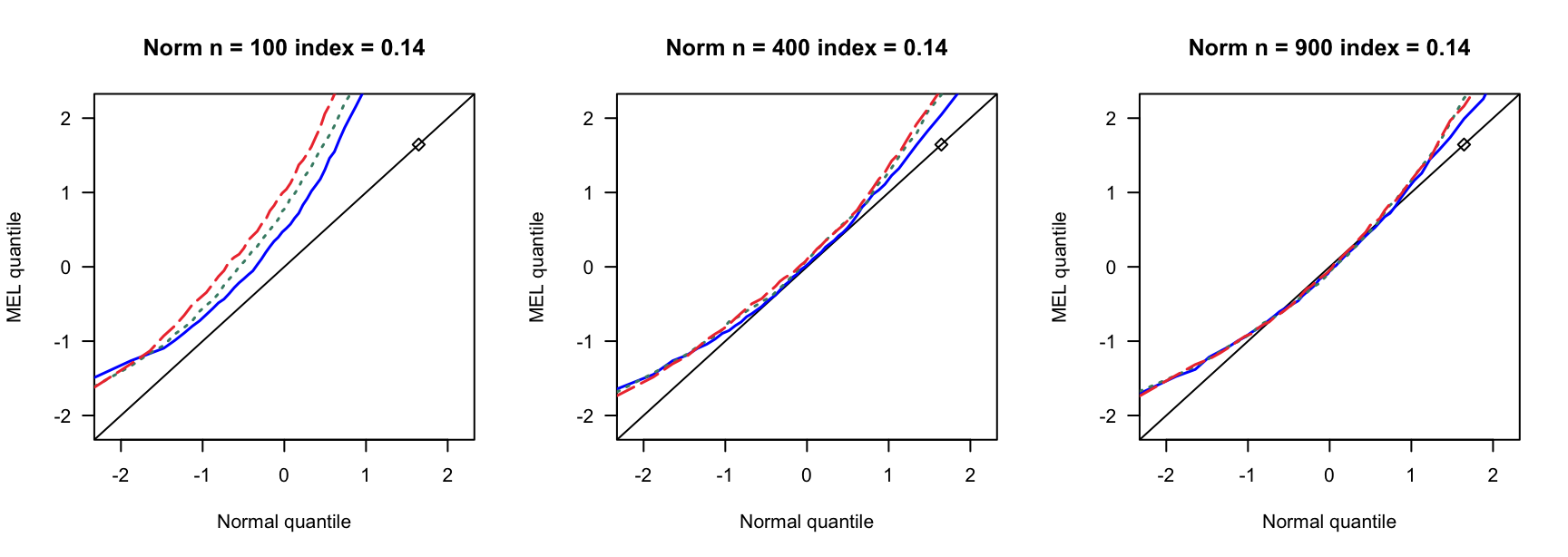
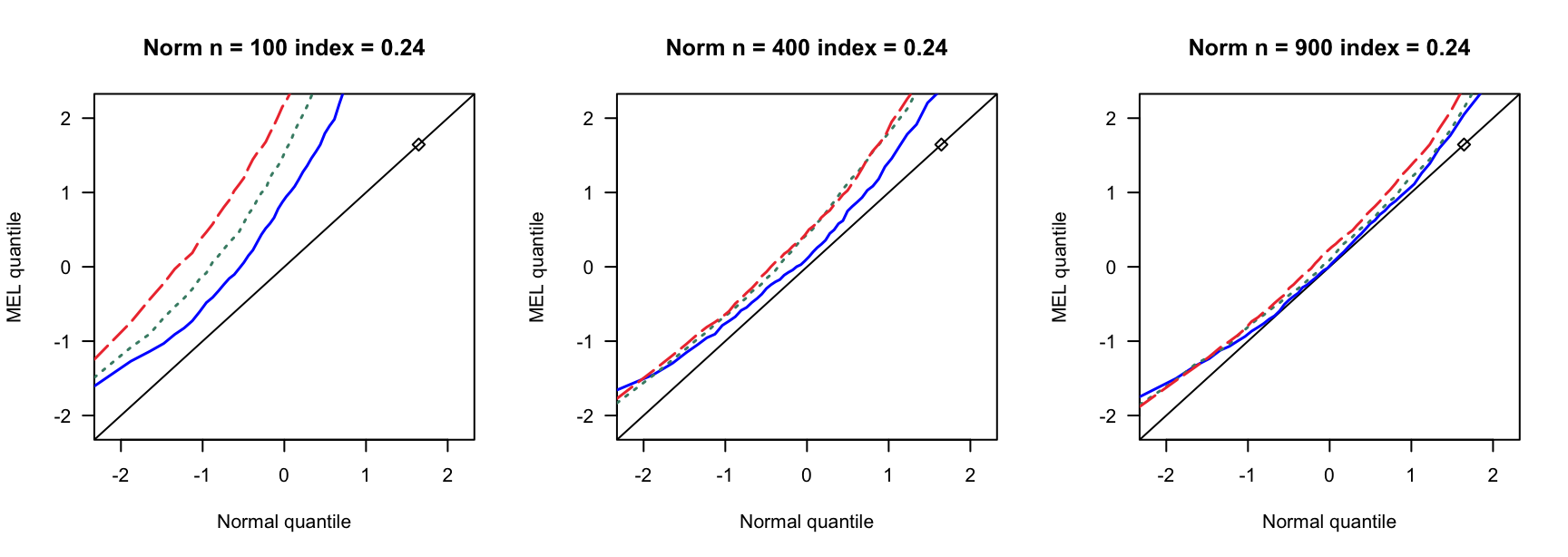
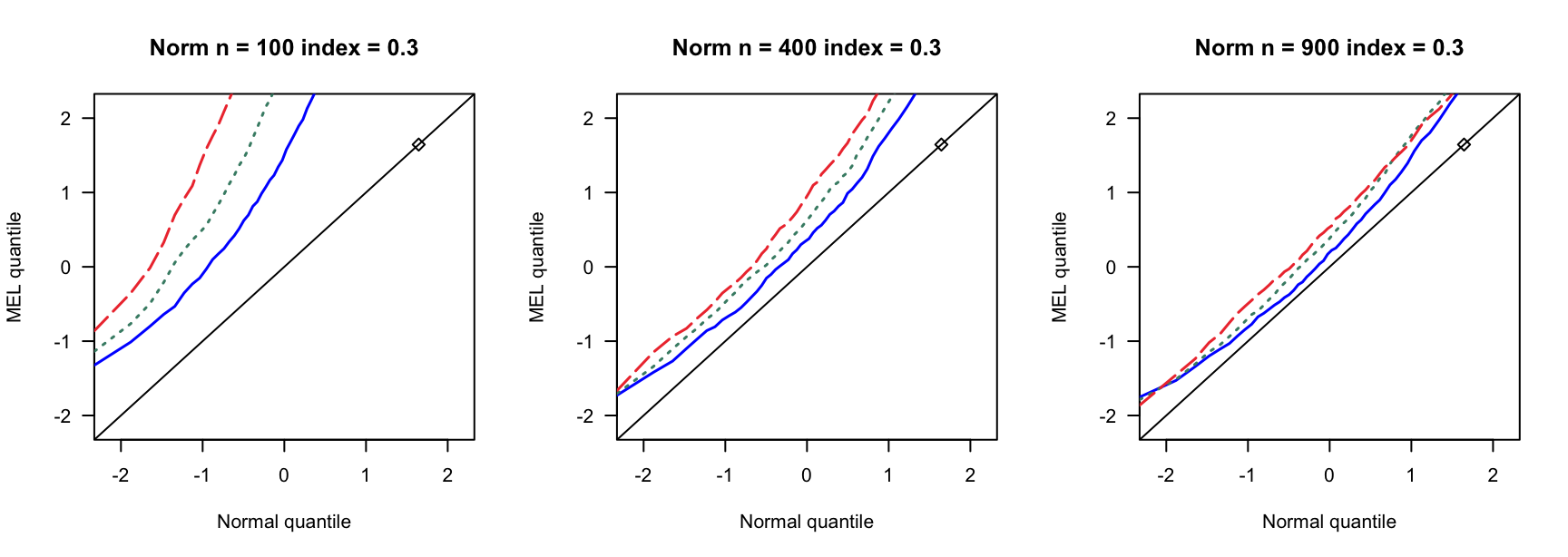
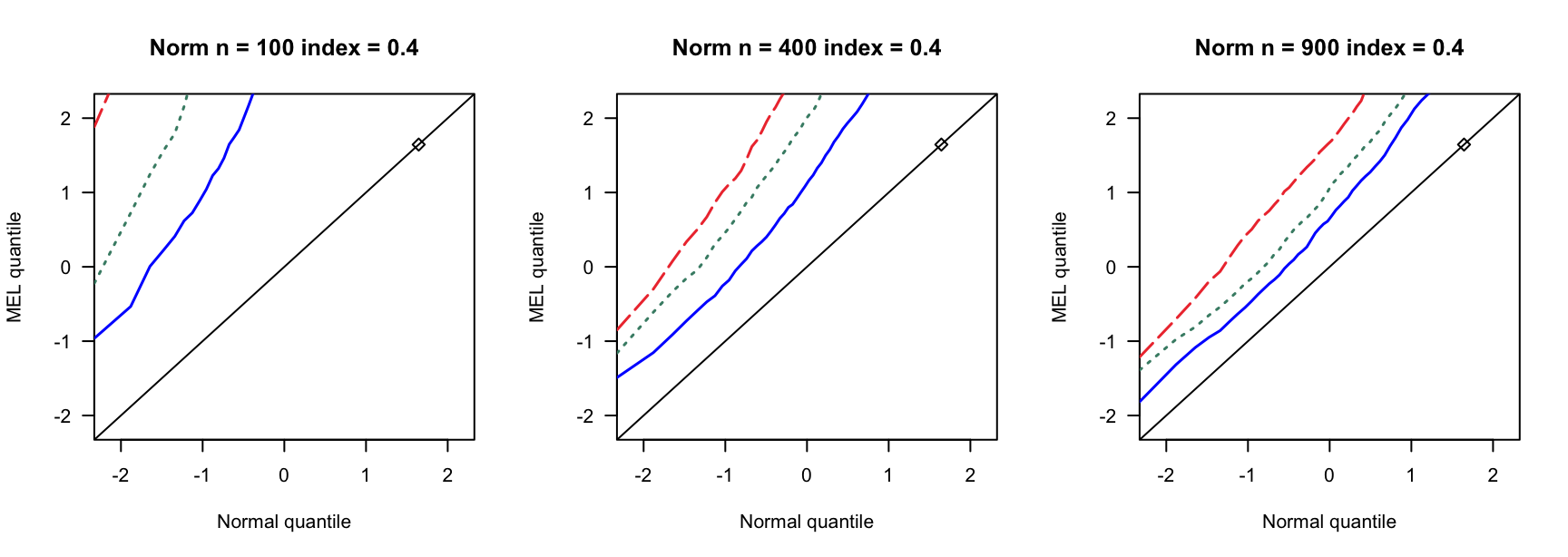
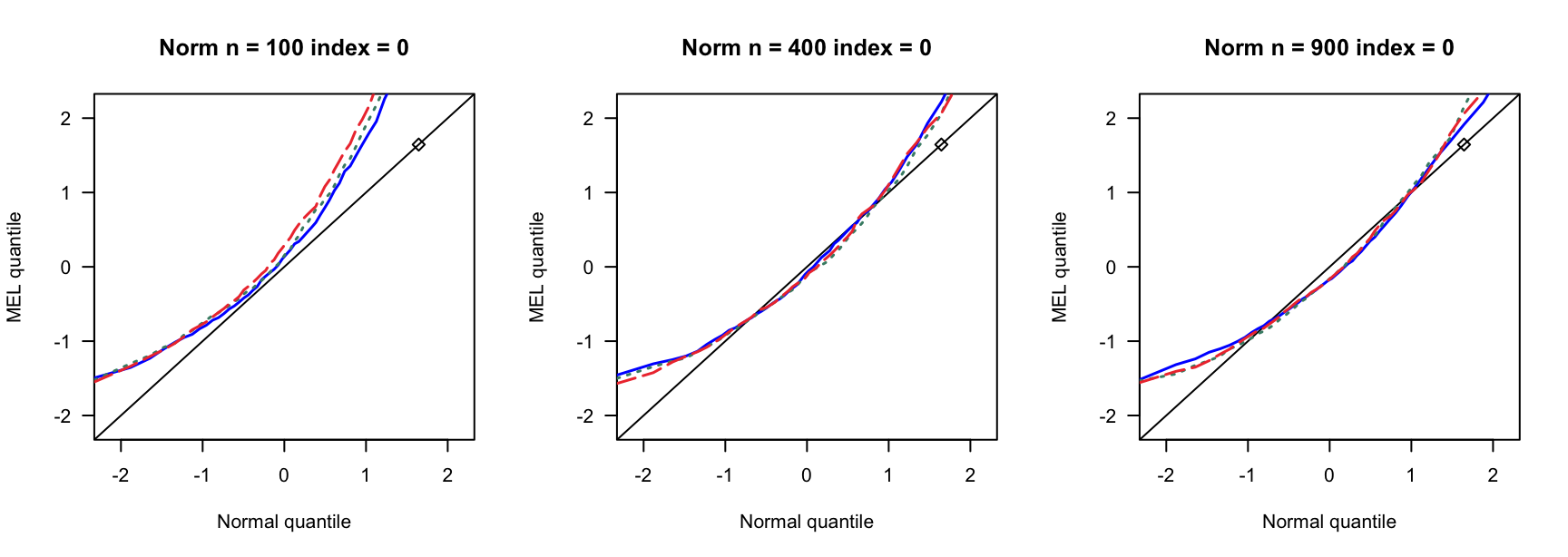
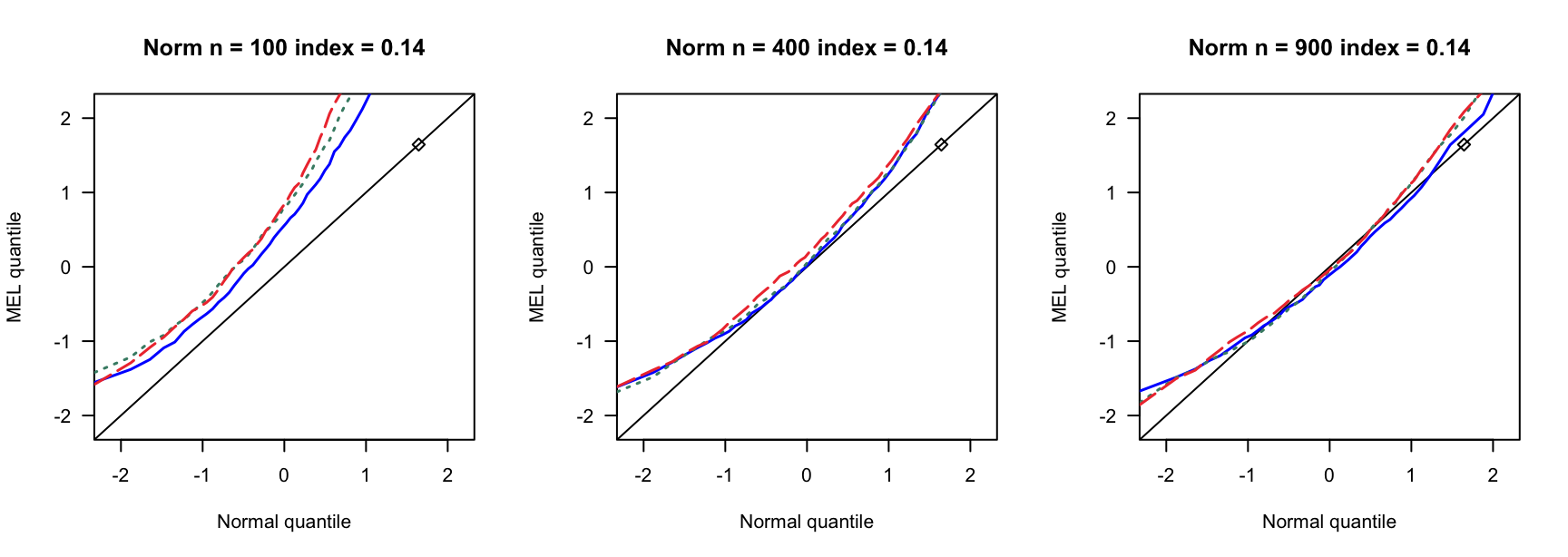
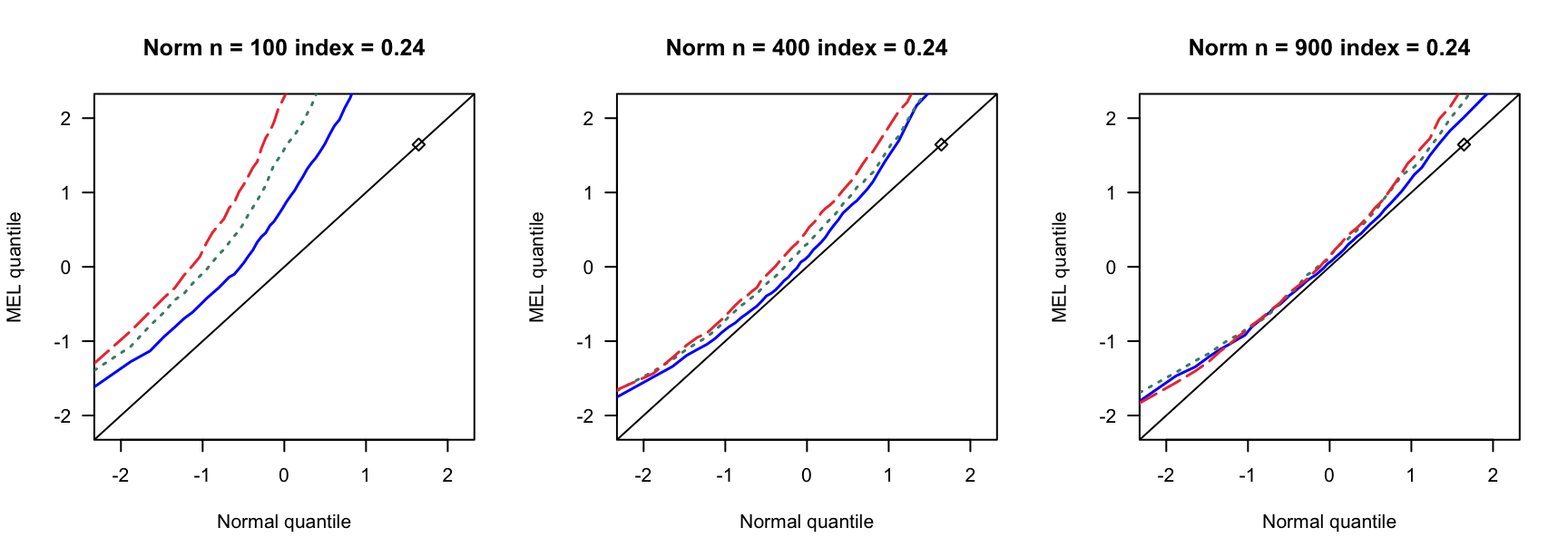
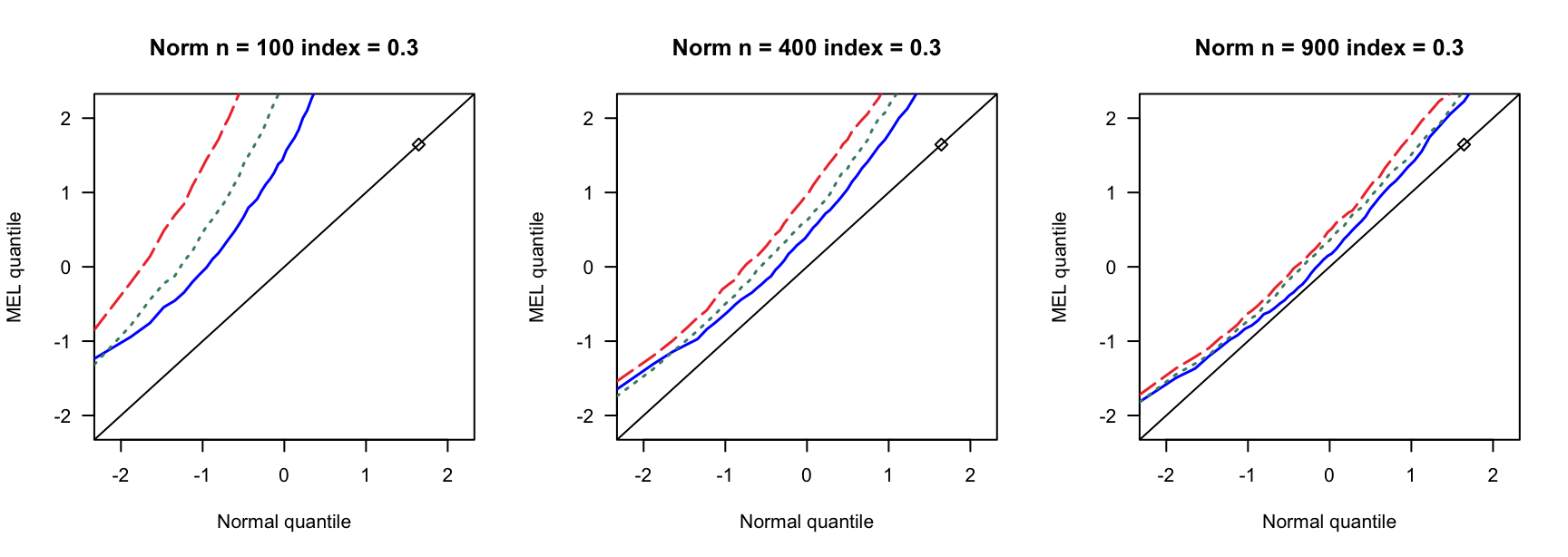
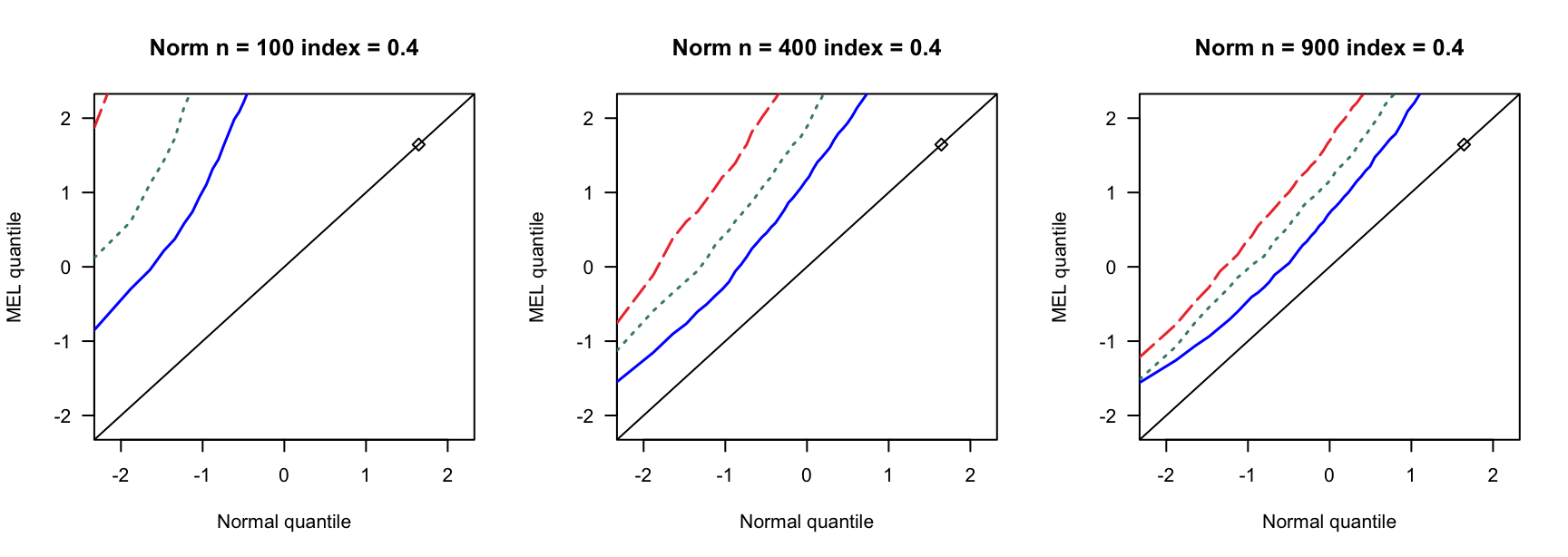
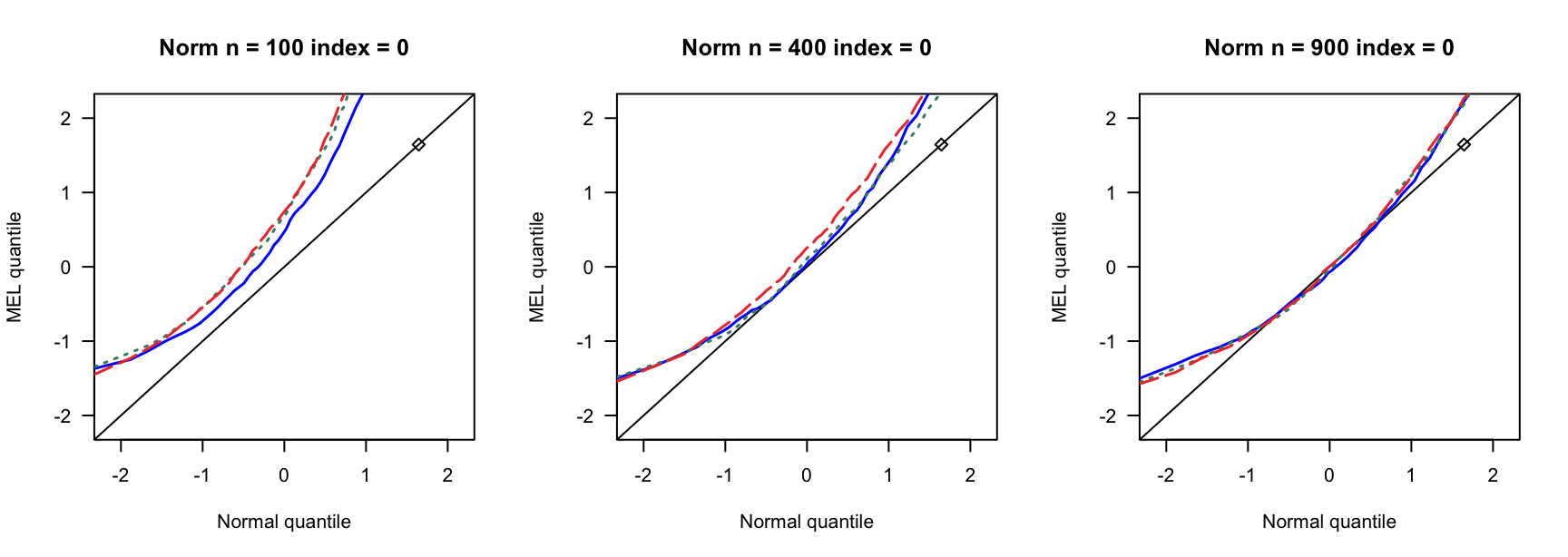
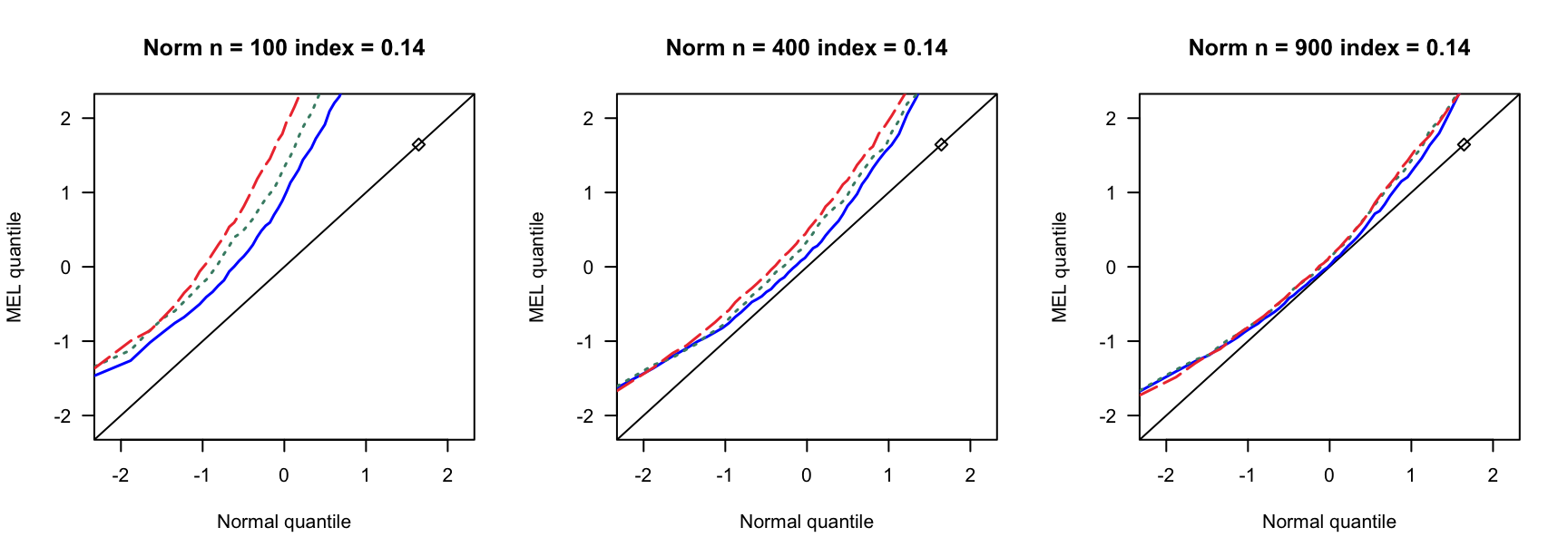
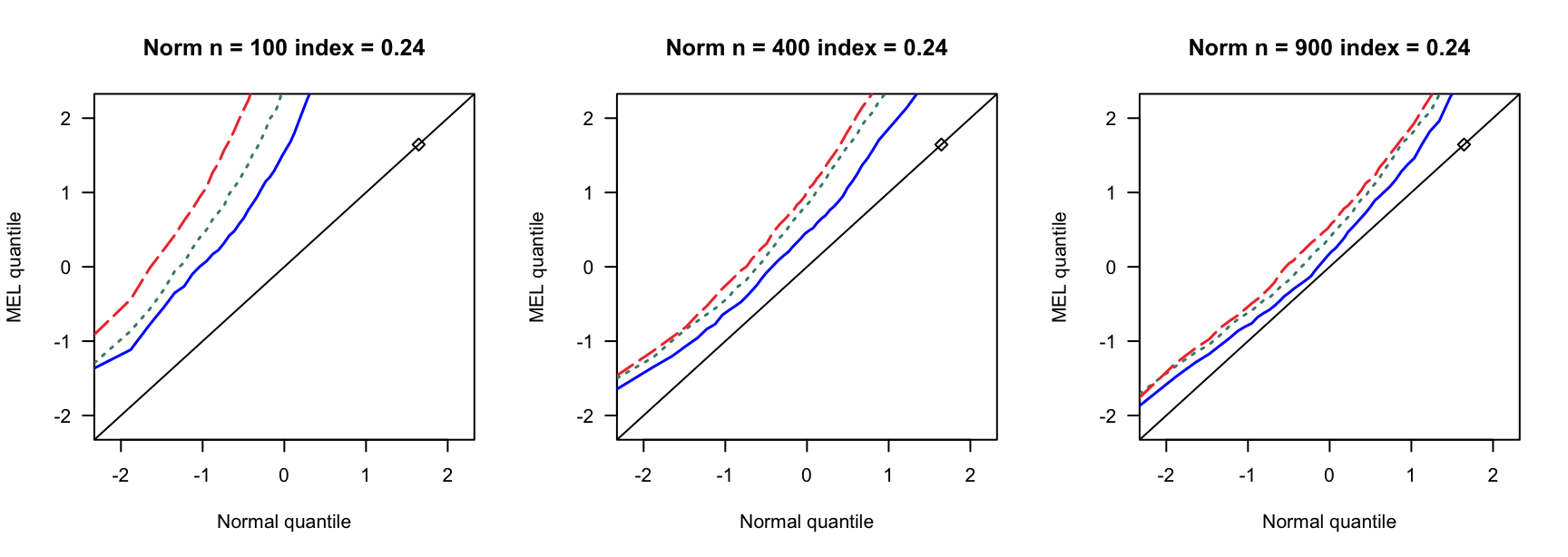
• \(N(0,1)\)误差

  	100	100	100	400	400	400	900	900	900
  0	3	0.890	0.892	3	0.931	0.935	3	0.954	0.955
  0	4	0.858	0.864	4	0.932	0.937	4	0.941	0.947
  0	5	0.821	0.829	5	0.922	0.932	5	0.938	0.943
  0.14	6	0.769	0.782	7	0.934	0.946	8	0.940	0.946
  0.14	8	0.721	0.738	9	0.911	0.919	10	0.923	0.931
  0.14	10	0.662	0.676	12	0.903	0.911	13	0.918	0.927
  0.24	9	0.697	0.722	13	0.896	0.916	15	0.934	0.940
  0.24	12	0.549	0.572	17	0.843	0.862	20	0.924	0.940
  0.24	15	0.433	0.459	21	0.833	0.846	26	0.904	0.910
  0.3	12	0.555	0.582	18	0.838	0.861	23	0.886	0.905
  0.3	16	0.360	0.380	24	0.778	0.803	31	0.843	0.872
  0.3	20	0.192	0.216	30	0.707	0.743	38	0.850	0.876
  0.4	19	0.280	0.301	33	0.651	0.690	46	0.791	0.822
  0.4	25	0.086	0.098	44	0.440	0.484	61	0.703	0.751
  0.4	32	0.008	0.010	55	0.275	0.312	76	0.518	0.578

• \(N(0,0.75)\)误差

	100	100	100	400	400	400	900	900	900
0	3	0.867	0.870	3	0.928	0.931	3	0.947	0.953
0	4	0.834	0.847	4	0.936	0.943	4	0.940	0.942
0	5	0.815	0.827	5	0.931	0.940	5	0.941	0.943
0.14	6	0.792	0.806	7	0.910	0.918	8	0.954	0.964
0.14	8	0.728	0.744	9	0.915	0.922	10	0.933	0.943
0.14	10	0.685	0.694	12	0.898	0.913	13	0.929	0.936
0.24	9	0.716	0.745	13	0.884	0.888	15	0.928	0.943
0.24	12	0.561	0.592	17	0.878	0.889	20	0.913	0.924
0.24	15	0.423	0.448	21	0.828	0.849	26	0.894	0.902
0.3	12	0.562	0.584	18	0.845	0.863	23	0.895	0.912
0.3	16	0.391	0.410	24	0.780	0.797	31	0.883	0.905
0.3	20	0.218	0.240	30	0.701	0.745	38	0.836	0.862
0.4	19	0.245	0.267	33	0.642	0.692	46	0.782	0.811
0.4	25	0.091	0.100	44	0.471	0.513	61	0.662	0.712
0.4	32	0.009	0.012	55	0.243	0.277	76	0.506	0.562

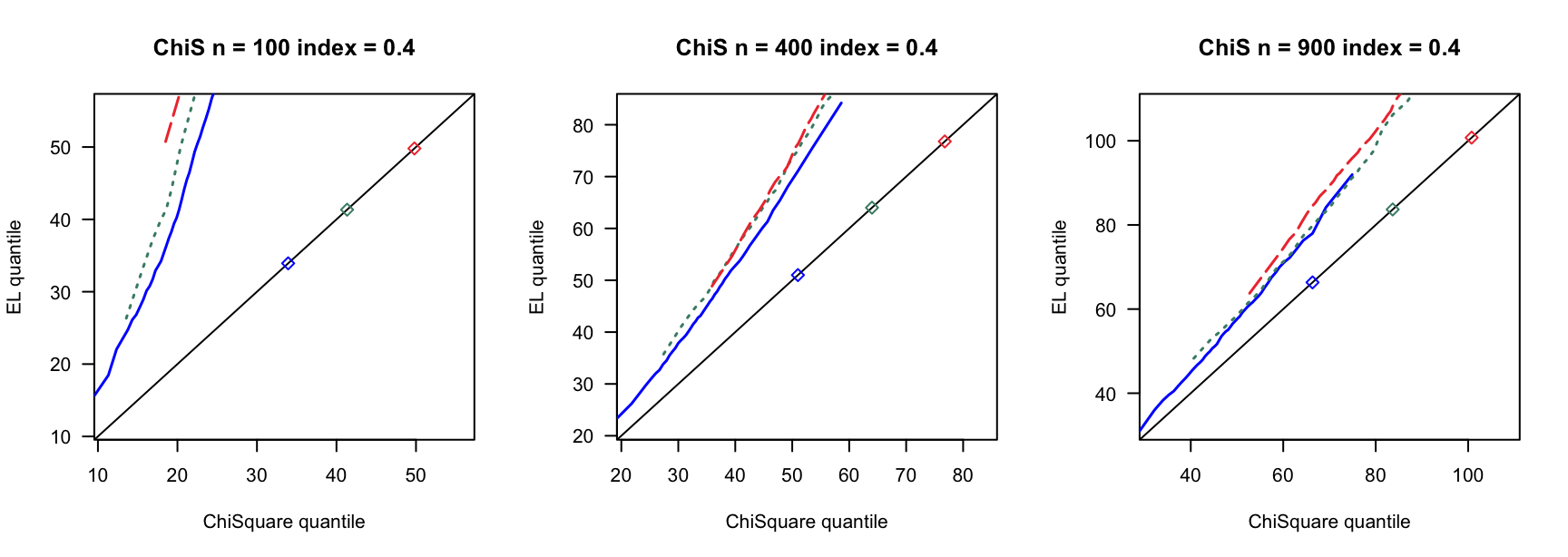
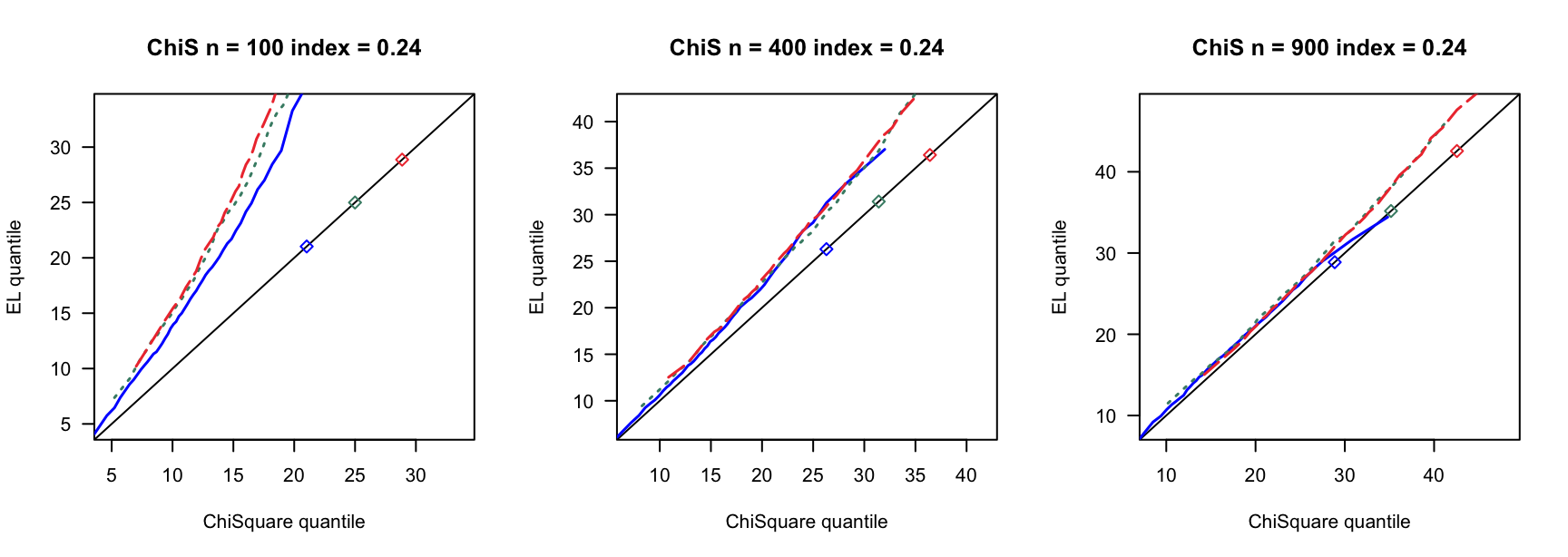
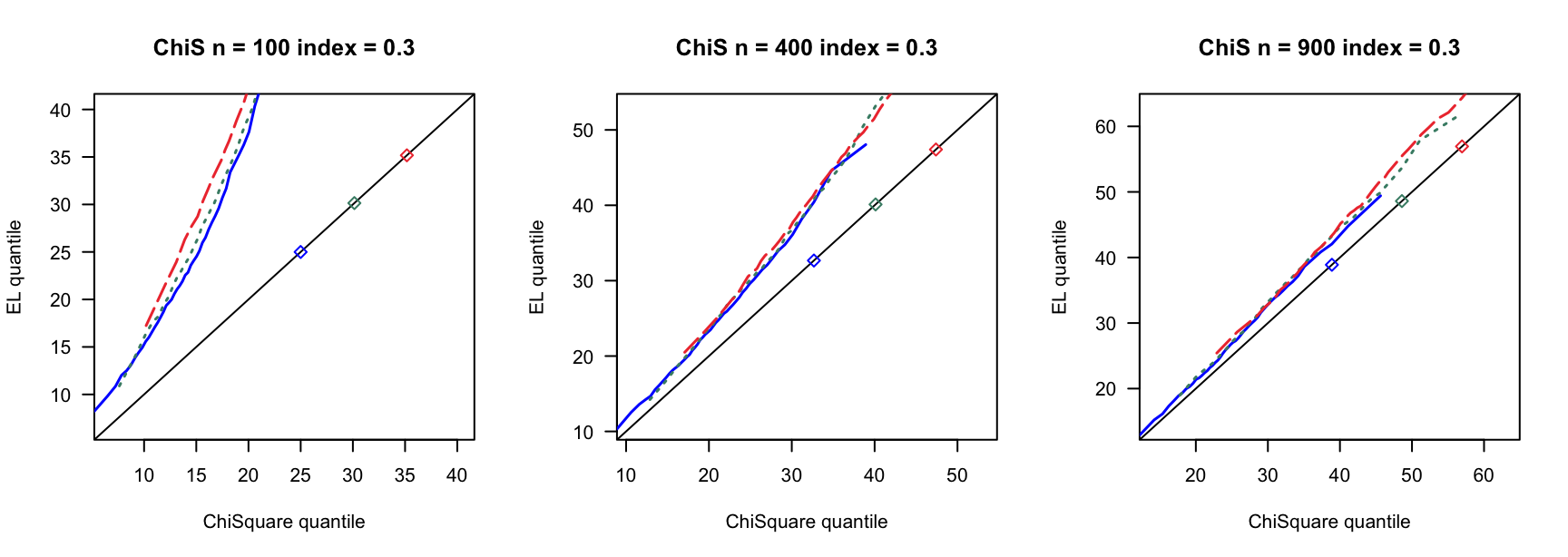
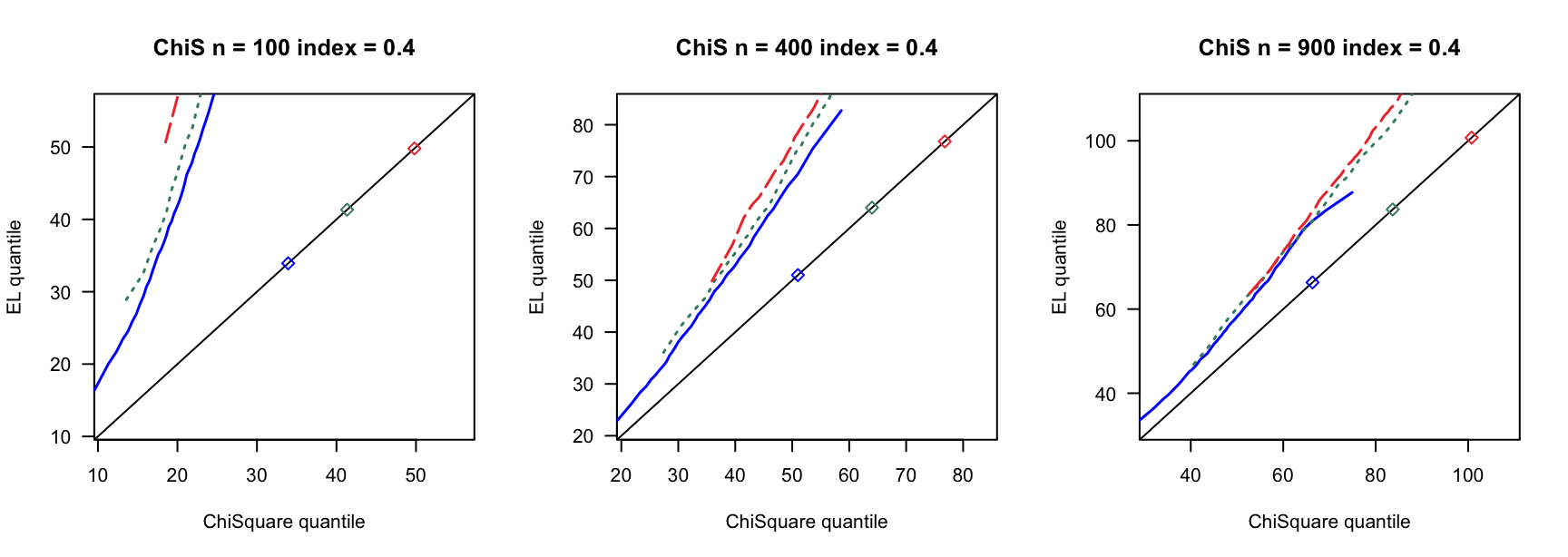
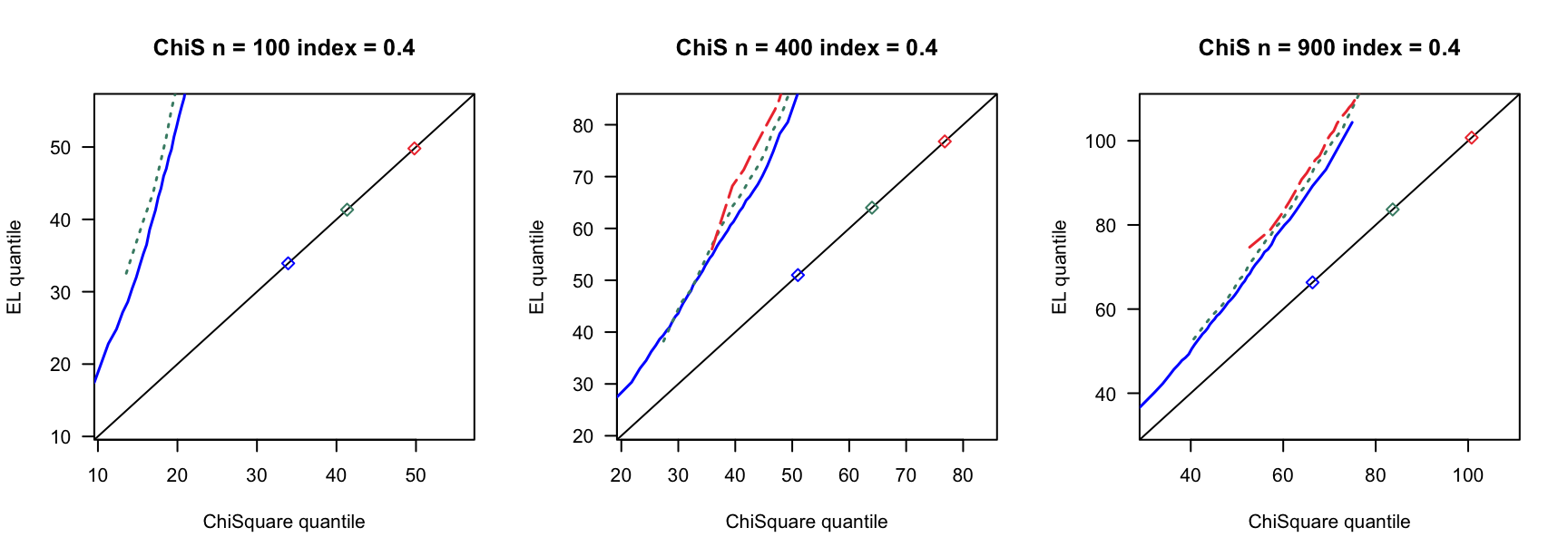
• \(t(5)\)误差

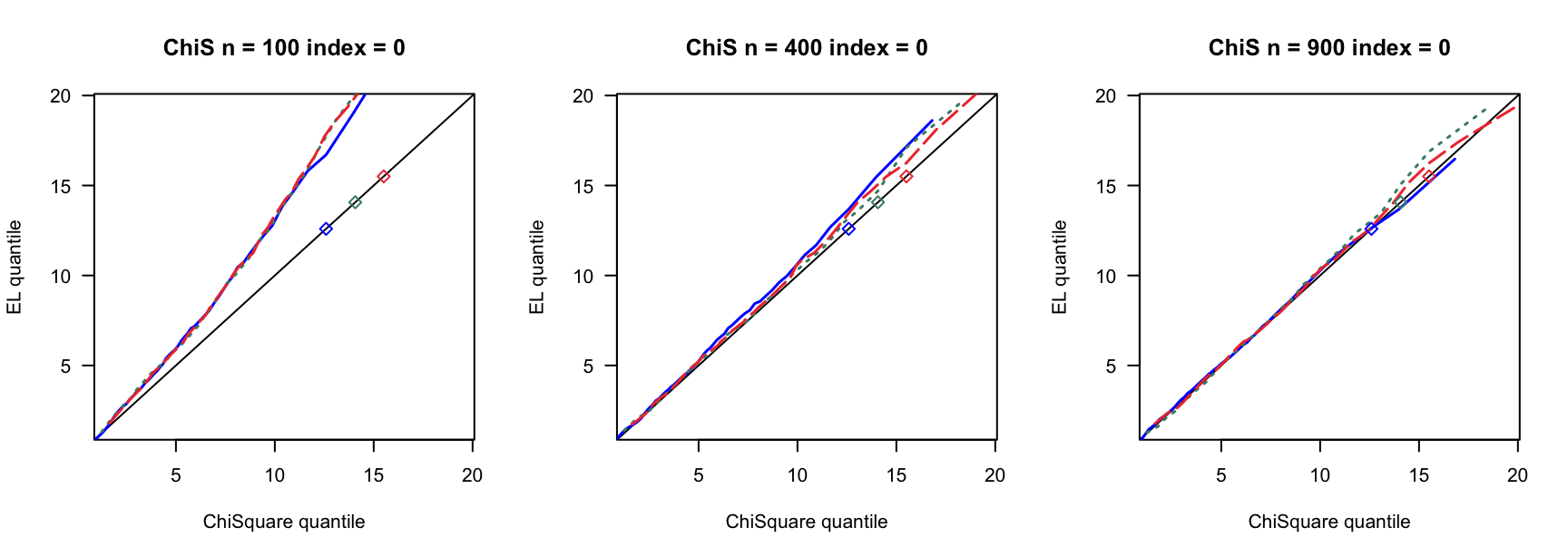
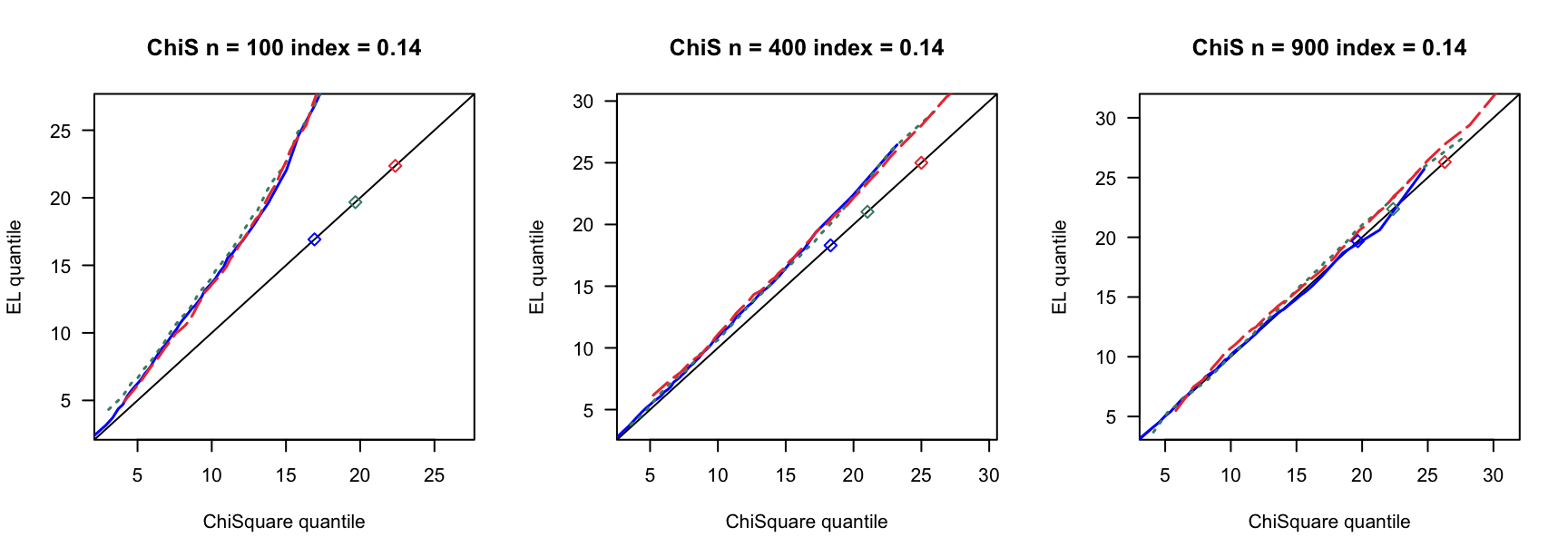
  	100	100	100	400	400	400	900	900	900
  0	3	0.780	0.789	3	0.894	0.903	3	0.928	0.930
  0	4	0.737	0.741	4	0.913	0.916	4	0.927	0.934
  0	5	0.716	0.727	5	0.879	0.891	5	0.922	0.932
  0.14	6	0.681	0.695	7	0.870	0.880	8	0.912	0.920
  0.14	8	0.585	0.605	9	0.853	0.868	10	0.889	0.906
  0.14	10	0.500	0.515	12	0.816	0.836	13	0.897	0.908
  0.24	9	0.555	0.570	13	0.834	0.858	15	0.888	0.904
  0.24	12	0.405	0.423	17	0.732	0.761	20	0.843	0.864
  0.24	15	0.267	0.285	21	0.683	0.719	26	0.827	0.850
  0.3	12	0.400	0.423	18	0.741	0.770	23	0.839	0.852
  0.3	16	0.237	0.258	24	0.617	0.658	31	0.772	0.814
  0.3	20	0.107	0.114	30	0.508	0.550	38	0.695	0.728
  0.4	19	0.152	0.165	33	0.421	0.466	46	0.617	0.668
  0.4	25	0.040	0.044	44	0.226	0.269	61	0.427	0.478
  0.4	32	0.003	0.004	55	0.088	0.108	76	0.239	0.284

• \(\chi^2(4)-4\)误差

  	100	100	100	400	400	400	900	900	900
  0	3	0.792	0.799	3	0.902	0.905	3	0.932	0.936
  0	4	0.770	0.778	4	0.891	0.897	4	0.928	0.933
  0	5	0.732	0.743	5	0.889	0.898	5	0.926	0.934
  0.14	6	0.699	0.709	7	0.874	0.882	8	0.922	0.929
  0.14	8	0.596	0.609	9	0.843	0.855	10	0.907	0.914
  0.14	10	0.500	0.528	12	0.828	0.849	13	0.889	0.902
  0.24	9	0.588	0.602	13	0.820	0.844	15	0.895	0.902
  0.24	12	0.445	0.463	17	0.781	0.801	20	0.868	0.887
  0.24	15	0.316	0.331	21	0.696	0.729	26	0.817	0.843
  0.3	12	0.466	0.486	18	0.726	0.760	23	0.856	0.876
  0.3	16	0.270	0.292	24	0.661	0.694	31	0.803	0.827
  0.3	20	0.169	0.185	30	0.532	0.574	38	0.748	0.785
  0.4	19	0.180	0.198	33	0.487	0.538	46	0.657	0.701
  0.4	25	0.052	0.061	44	0.285	0.326	61	0.484	0.537
  0.4	32	0.008	0.011	55	0.137	0.166	76	0.294	0.357

5.2 分位数图

5.2.1 \(N(0,1)\)误差 EL

5.2.2 \(N(0,1)\)误差 MEL

5.2.3 \(N(0,0.75)\)误差 EL

5.2.4 \(N(0,0.75)\)误差 MEL

5.2.5 \(t(5)\)误差 EL

5.2.6 \(t(5)\)误差 MEL

5.2.7 \(\chi^2(4)-4\)误差 EL

5.2.8 \(\chi^2(4)-4\)误差 MEL